Fagaras, в свою очередь, обеспечивает формирование узла Bucharest, который является целевым. Применение в процессе решения данной конкретной задачи алгоритма жадного поиска по первому наилучшему совпадению с использованием функциипозволяет найти решение без развертывания какого-либо узла, не находящегося в пути решения; это означает, что стоимость такого поиска является минимальной. Но само найденное решение не оптимально: путь до Бухареста через города Сибиу и Фэгэраш на 32 километра длиннее, чем путь через города Рымнику-Вылча и Питешти. Это замечание показывает, почему данный алгоритм называется "жадным": на каждом этапе он пытается подойти к цели как можно ближе (фигурально выражаясь, "захватить как можно больше").

Рис. 4.1. Этапы жадного поиска пути до Бухареста по первому наилучшему совпадению с использованием эвристической функции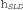., определяющей расстояние по прямой. Узлы обозначены с помощью их h-значений

Процедура минимизации h[n) восприимчива к фальстартам (при ее использовании иногда приходится отменять начальные этапы). Рассмотрим задачу поиска пути от города Яссы до города Фэгэраш. Эта эвристическая функция подсказывает, что в первую очередь должен быть развернут узел города Нямц, Neamt, поскольку он является ближайшим к узлу Fagaras, но этот путь становится тупиковым. Решение состоит в том, чтобы отправиться вначале в город Васлуй (а этот этап, согласно данной эвристической функции, фактически уводит дальше от цели), а затем продолжать движение через Урзичени, Бухарест и, наконец, в Фэгэраш. Поэтому в данном случае применение указанной эвристической функции вызывает развертывание ненужных узлов. Более того, если не будет предусмотрено обнаружение повторяющихся состояний, то решение так никогда не будет найдено — процедура поиска станет совершать возвратно-поступательные движения между узлами Neamt и lasi.

Жадный поиск по первому наилучшему совпадению напоминает поиск в глубину в том отношении, что этот алгоритм предпочитает на пути к цели постоянно следовать по единственному пути, но возвращается к предыдущим узлам после попадания в тупик. Данный алгоритм страдает от тех же недостатков, что и алгоритм поиска в глубину: он не является оптимальным, к тому же он — не полный (поскольку способен отправиться по бесконечному пути, да так и не вернуться, чтобы опробовать другие возможности). При этом в наихудшем случае оценки временной и пространственной сложности составляют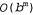, где т — максимальная глубина пространства поиска. Однако хорошая эвристическая функция позволяет существенно сократить такую сложность. Величина этого сокращения зависит от конкретной задачи и от качества эвристической функции.