|
Страница 1 из 5 Формально говоря, любая задача удовлетворения ограничений (Constraint Satisfaction Problem — CSP) определена множеством переменных,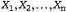 , и множеством ограничений, , и множеством ограничений,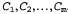 . Каждая переменная хi имеет непустую область определения . Каждая переменная хi имеет непустую область определения возможных значений. Каждое ограничение Сi включает некоторое подмножество переменных и задает допустимые комбинации значений для этого подмножества. Состояние задачи определяется путем присваивания значений некоторым или всем этим переменным, возможных значений. Каждое ограничение Сi включает некоторое подмножество переменных и задает допустимые комбинации значений для этого подмножества. Состояние задачи определяется путем присваивания значений некоторым или всем этим переменным,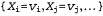 . Присваивание, которое не нарушает никаких ограничений, называется совместимым, или допустимым присваиванием. Полным называется такое присваивание, в котором участвует каждая переменная, а решением задачи CSP является полное присваивание, которое удовлетворяет всем ограничениям. Кроме того, для некоторых задач CSP требуется найти решение, которое максимизирует целевую функцию. . Присваивание, которое не нарушает никаких ограничений, называется совместимым, или допустимым присваиванием. Полным называется такое присваивание, в котором участвует каждая переменная, а решением задачи CSP является полное присваивание, которое удовлетворяет всем ограничениям. Кроме того, для некоторых задач CSP требуется найти решение, которое максимизирует целевую функцию. Как же все это описание перевести на язык практики? Предположим, что устав от Румынии, мы рассматриваем карту Австралии, на которой показаны все ее штаты и территории (рис. 5.1, a), и что мы получили задание раскрасить каждый регион в красный, зеленый или синий цвет таким способом, чтобы ни одна пара соседних регионов не имела одинаковый цвет. Чтобы сформулировать это задание в виде задачи CSP, определим в качестве переменных сокращенные обозначения этих регионов: wa, NT, О, NSW, V, SA и т. Областью определения каждой переменной является множество цветов {red, green, blue). Ограничения требуют, чтобы все пары соседних регионов имели разные цвета; например, допустимыми комбинациями для WA и NT являются следующие пары: 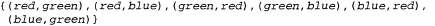
(Это ограничение можно также представить более сжато в виде неравенства 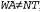 , при условии, что в данном алгоритме удовлетворения ограничений предусмотрен некоторый способ вычисления таких выражений.) Количество возможных решений достаточно велико; например, одним из таких решений является следующее: , при условии, что в данном алгоритме удовлетворения ограничений предусмотрен некоторый способ вычисления таких выражений.) Количество возможных решений достаточно велико; например, одним из таких решений является следующее: 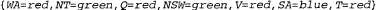
Задачу CSP удобно представить визуально в виде графа ограничений, как показано на рис. 5.1, б. Узлы этого графа соответствуют переменным задачи, а дуги — ограничениям.
<< В начало < Предыдущая 1 2 3 4 5 Следующая > В конец >>
|