Равновесие между риском и вознаграждением изменяется в зависимости от значения функции R{s) для нетерминальных состояний. На рис. 17.2, б показаны оптимальные стратегии для четырех различных диапазонов изменения значения R(s). Если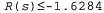, жизнь настолько мучительна, что агент направляется прямо к ближайшему выходу, даже если стоимость этого выхода равна -1. Если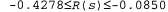, жизнь довольно дискомфортна; агент выбирает кратчайший маршрут к состоянию +1 и стремится избежать риска случайного попадания в состояние -1. В частности, агент выбирает короткий путь из квадрата (3,1). А если жизнь не так уж неприятна, оптимальная стратегия состоит в том, чтобы избегать вообще какого-либо риска. В квадратах (4,1) и (3,2) агент направляется буквально прочь от состояния -1, чтобы случайно не попасть туда ни при каких обстоятельствах, даже несмотря на то, что из-за этого ему приходится несколько раз удариться головой о стену. Наконец, если R( s) >0, то жизнь агента становится весьма приятной и он избегает обоих выходов. При условии, что используются действия, показанные в квадратах (4,1), (3,2) и (3,3), любая стратегия является оптимальной и агент получает бесконечно большое суммарное вознаграждение, поскольку он никогда не попадает в терминальное состояние. Как это ни удивительно, но оказывается, что существуют шесть других оптимальных стратегий для различных диапазонов значений R (s); в упр. 17.7 предлагается найти эти стратегии.

Рис. 17.2. Примеры оптимальных стратегий: оптимальная стратегия для стохастической среды со значениями R(s) = -0.04 в нетерминальных состояниях (а); оптимальные стратегии для четырех различных диапазонов значений R (s) (б)

Тщательное уравновешивание риска и вознаграждения является характерной особенностью задач MDP, которая не возникает в детерминированных задачах поиска; более того, такое уравновешивание характерно для многих реальных задач принятия решений. По этой причине задачи MDP изучаются в нескольких научных областях, включая искусственный интеллект, исследование операций, экономику и теорию управления. Для вычисления оптимальных стратегий были предложены десятки алгоритмов. В разделах 17.2 и 17.3 описываются два наиболее важных семейства алгоритмов. Но вначале мы должны завершить начатое исследование полезно-стей и стратегий для задач последовательного принятия решений.