В ядерной модели каждый обучающий экземпляр рассматривается как самостоятельно вырабатывающий небольшую функцию плотности (ядерную функцию). Оценка всей плотности в целом представляет собой нормализованную сумму всех небольших ядерных функций. Обучающий экземпляр в точке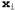вырабатывает ядерную функцию, которая присваивает определенную вероятность каждой точке χ в пространстве. Поэтому оценка плотности принимает такой вид:

Ядерная функция обычно зависит только от расстояниямежду точкой χ и экземпляром. Наиболее широко применяемой ядерной функцией (безусловно) является гауссово распределение. Для упрощения предполагается использование сферического гауссова распределения со среднеквадратичным отклонением w вдоль каждой оси, т.е. следующего распределения:

где d — количество размерностей в точке х. И при таком подходе все еще приходится сталкиваться с проблемой выбора подходящего значения для w, как и прежде, применение слишком малой окрестности приводит к получению оценки, состоящей из слишком большого количества пиков, как показано на рис. 20.14, а. На рис. 20.14, б видно, что промежуточное значение w позволяет получить очень хорошую реконструкцию первоначального распределения. А на рис. 20.14, в применение слишком большой окрестности приводит к полной потере структуры. Хорошее значение w может быть выбрано с использованием перекрестной проверки.

Рис. 20.14. Оценка плотности с помощью ядерной модели для данных, показанных на рис. 20.12, а, в которых используется ядерная функция гауссова распределения со значениями w=0 . 02, 0.07 и 0.20

Контролируемое обучение с помощью ядерных функций осуществляется путем взятия взвешенных комбинаций всех предсказаний из обучающих экземпляров (сравните такой подход с предсказанием с помощью к ближайших соседних точек, в котором берется невзвешенная комбинация ближайших к экземпляров). Вес i-ro экземпляра для точки запроса χ определяется по значению ядерной функции . Для предсказания в дискретном случае можно выполнить взвешенное голосование, а для предсказания в непрерывном случае — получить взвешенное среднее или применить метод взвешенной линейной регрессии. Следует отметить, что для получения предсказаний с помощью ядерной функции требуется анализ каждого обучающего экземпляра. Существует также возможность объединять ядерные функции со схемами индексации ближайших соседних точек для получения взвешенных предсказаний только с помощью самых близких экземпляров.