Приведенное выше описание нейронных сетей не дает ответа на одну дилемму. Однослойные сети позволяют использовать простой и эффективный алгоритм обучения, но обладают лишь очень ограниченной выразительной мощью, поскольку способны определять в процессе обучения только линейные границы между решениями в пространстве входов. Многослойные сети, с другой стороны, являются гораздо более выразительными (они способны представлять нелинейные функции общего вида), но задача их обучения становится очень сложной из-за большого количества локальных минимумов и высокой размерности пространства весов. В этом разделе рассматривается относительно новое семейство методов обучения, основанных на использовании машин поддерживающих векторов (Support Vector Machine— SVM), или, в более общем смысле, ядерных машин (kernel machine). Ядерные машины позволяют в определенной степени воспользоваться наилучшими свойствами и однослойных, и многослойных сетей. Это означает, что в методах, основанных на их использовании, предусмотрен эффективный алгоритм обучения, а сами они позволяют представить сложные, нелинейные функции.

Полное описание ядерных машин выходит за рамки данной книги, но мы можем проиллюстрировать их основную идею на примере. На рис. 20.25, а показано двухмерное пространство входов, определяемое атрибутами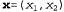, в котором положительные примеры (у=+1) находятся внутри круга, а отрицательные примеры (у=-1)— вне его. Очевидно, что для данной задачи не существует линейного разделителя. А теперь предположим, что входные данные выражены иначе, с помощью каких-то вычислимых характеристик, т.е. что каждый вектор входных данных χ отображен на новый вектор значений характеристик, F(x). В частности, предположим, что используются следующие три характеристики:

(20.16)

Вскоре будет показано, как получены эти выражения, а пока просто рассмотрим, что происходит. На рис. 20.25, б показаны данные в этом новом, трехмерном пространстве, определенном тремя характеристиками; очевидно, что данные в этом пространстве являются линейно разделимыми! Такой подход действительно является достаточно общим: если данные отображаются на пространство с достаточно большим количеством размерностей, то они всегда могут быть преобразованы в линейно разделимую форму. В данном случае использовались только три размерности14, но если бы количество точек данных было равно N, то, за исключением частных случаев, они всегда являются разделимыми в пространстве с N-1 размерностями или больше (упр. 20.21).

Рис. 20.25. Пример применения преобразования: двухмерная задача обучения с положительными примерами, показанными в виде черных кружков, и отрицательными примерами, обозначенными белыми кружками. Показана также истинная граница решений,(а); те же данные после отображения на трехмерное пространство входов Круглая граница решений, показанная на рис. 20.25, а, в трехмерном пространстве становится линейной границей решения (б)