Следующий этап, который теперь должен стать полностью очевидным, состоит в демонстрации того, что в ядерной функции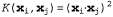нет ничего особенного, просто она соответствует конкретному пространству характеристик с большим количеством размерностей, а другие ядерные функции соответствуют другим пространствам характеристик. Один из знаменитых результатов в математике, теорема Мерсера [1035], гласит, что любая "приемлемая" ядерная функция соответствует некоторому пространству характеристик. Эти пространства характеристик могут оказаться очень большими даже применительно к таким ядерным функциям, которые выглядят совершенно "невинно". 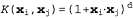Например, полиномиальная ядерная функция, , соответствует пространству характеристик, количество размерностей которого определяется экспоненциальной зависимостью от d. Поэтому использование ядерных функций, подобных приведенной в уравнении 20.17, обеспечивает эффективный поиск оптимальных линейных разделителей в пространствах характеристик с миллиардами (а в некоторых случаях с бесконечным количеством) размерностей. Полученные в результате линейные разделители после их обратного отображения на первоначальное пространство входов могут соответствовать произвольно сложным, нелинейным границам между положительными и отрицательными примерами.

Как было упомянуто в предыдущем разделе, ядерные машины превосходят все другие способы распознавания рукописных цифр; кроме того, они быстро находят применение и в других приложениях, особенно в тех, которые отличаются большим количеством входных характеристик. В составе этого процесса было разработано много новых ядерных функций, позволяющих работать со строками, деревьями и другими нечисловыми типами данных. Было также отмечено, что метод ядерных функций может применяться не только в алгоритмах обучения, которые находят оптимальные линейные разделители, но и в любых других алгоритмах, которые можно переформулировать применительно к использованию только точечных произведений пар точек данных, как в уравнениях 20.17 и 20.18. После выполнения такого преобразования точечное произведение заменяется ядерной функцией, что приводит к получению версии того же алгоритма, преобразованной в ядерную форму. Кроме всего прочего, такое преобразование можно легко применить для обучения с к ближайшими соседними точками и для обучения персептрона.