|
Страница 2 из 4 Итак, можно ли считать, что на этом проблема исчерпана? Достаточно ли просто подготовить целый ряд расчетных характеристик, а затем найти линейный разделитель в соответствующем многомерном пространстве? К сожалению, все не так просто. Напомним, что линейный разделитель в пространстве с d размерностями определяется уравнением с d параметрами, поэтому возникает серьезная опасность чрезмерно тщательной подгонки данных, если 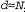 т.е. приблизительно равно количеству точек данных. (Такая ситуация аналогична чрезмерно тщательной подгонке к данным с помощью полинома высокой степени, о чем шла речь в главе 18.) По этой причине ядерные машины обычно находят оптимальный линейный разделитель, т.е. такой разделитель, который имеет наибольший край между ним и положительными примерами, с одной стороны, и отрицательными примерами, с другой (рис. 20.26). Можно показать, используя аргументы, основанные на теории вычислительного обучения (см. раздел 18.5), что такой разделитель обладает желаемыми свойствами с точки зрения возможности надежного обобщения новых примеров. т.е. приблизительно равно количеству точек данных. (Такая ситуация аналогична чрезмерно тщательной подгонке к данным с помощью полинома высокой степени, о чем шла речь в главе 18.) По этой причине ядерные машины обычно находят оптимальный линейный разделитель, т.е. такой разделитель, который имеет наибольший край между ним и положительными примерами, с одной стороны, и отрицательными примерами, с другой (рис. 20.26). Можно показать, используя аргументы, основанные на теории вычислительного обучения (см. раздел 18.5), что такой разделитель обладает желаемыми свойствами с точки зрения возможности надежного обобщения новых примеров.  Рис. 20.26. Замыкание оптимального разделителя, показанного на рис. 20.25, 6, спроектированное на первые две размерности. Разделитель показан в виде жирной линии, а ближайшие тонки (поддерживающие векторы) обозначены кружками. Край представляет собой разделение между положительными и отрицательными примерами Но как найти такой разделитель? Оказалось, что эта задача представляет собой задачу оптимизации из области квадратичного программирования. Предположим, что имеются примеры 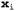 с классификациями с классификациями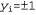 и необходимо найти оптимальный разделитель в пространстве входов; в таком случае задача квадратичного программирования сводится к поиску значений параметров и необходимо найти оптимальный разделитель в пространстве входов; в таком случае задача квадратичного программирования сводится к поиску значений параметров , которые максимизируют следующее выражение с учетом ограничений , которые максимизируют следующее выражение с учетом ограничений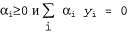 : :  (20.17) (20.17)
Хотя для понимания излагаемого материала не обязательно знакомиться с тем, как было выведено данное выражение, следует отметить, что оно имеет два важных свойства. Во-первых, это выражение имеет единственный глобальный максимум, который может быть найден с помощью эффективных методов. Во-вторых, данные входят в это выражение только в форме точечных произведений пар точек. Утверждение о существовании такого второго свойства является также справедливым применительно к уравнению для самого разделителя; как только будут вычислены оптимальные значения аь появляется возможность вычислить следующее выражение:  (20.18) (20.18)
|