|
Страница 2 из 2 Но для некоторых видов функций такая проблема становится вполне реальной. Например, если рассматриваемая функция является функцией определения четности, которая возвращает 1 тогда и только тогда, когда на входах задано четное количество единиц, то потребуется дерево решений, имеющее экспоненциальную величину. Кроме того, сложной является задача использования дерева решений для представления мажоритарной функции, которая возвращает 1, если больше чем на половине ее входов имеется 1. Иными словами, деревья решений вполне подходят для функций одних типов и не подходят для других. Существует ли представление какого-либо типа, являющееся эффективным для функций всех типов? К сожалению, ответ на этот вопрос отрицателен. Это утверждение можно доказать с помощью такого общего способа. Рассмотрим множество всех булевых функций от η атрибутов. Каково общее количество различных функций в этом множестве? Оно определяется количеством различных истинностных таблиц, которые могут быть составлены на этих атрибутах, поскольку функция определятся своей истинностной таблицей. Истинностная таблица имеет  строк, так как для описания вариантов входных данных применяется η атрибутов. Столбец "ответов" такой таблицы может рассматриваться как число, состоящее из строк, так как для описания вариантов входных данных применяется η атрибутов. Столбец "ответов" такой таблицы может рассматриваться как число, состоящее из 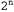 битов, которое определяет функцию. Независимо от того, какое представление используется для функций, некоторые из функций (а фактически почти все) должны потребовать для своего представления именно такое количество битов. битов, которое определяет функцию. Независимо от того, какое представление используется для функций, некоторые из функций (а фактически почти все) должны потребовать для своего представления именно такое количество битов. Если для определения функции требуется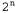 битов, то существует битов, то существует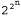 различных функций от η атрибутов. Это число является весьма обескураживающим. Например, при наличии лишь шести булевых атрибутов существует различных функций от η атрибутов. Это число является весьма обескураживающим. Например, при наличии лишь шести булевых атрибутов существует 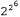 = 18 446 744 073 709 551 616 различных функций, из числа которых может быть сделан выбор. Для поиска совместимых гипотез в таком большом пространстве потребуется некоторые остроумные алгоритмы. = 18 446 744 073 709 551 616 различных функций, из числа которых может быть сделан выбор. Для поиска совместимых гипотез в таком большом пространстве потребуется некоторые остроумные алгоритмы.
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|