Задача, приведенная в листинге 12.1, может быть решена с помощью любого из планировщиков, которые уже описывались в настоящей книге. На рис. 12.1 показано решение, которое было бы получено с помощью планировщика POP с частичным упорядочением (если игнорируются некоторые числовые данные). Теперь для преобразования этой задачи в задачу составления расписания, а не в задачу планирования, необходимо определить, когда должно начаться и закончиться каждое действие, с учетом продолжительности действия, а также их упорядочения. Обозначение Duration (d) в спецификации результата действия (где переменная d должна быть привязана к некоторому числу) показывает, что для выполнения действия требуется d минут.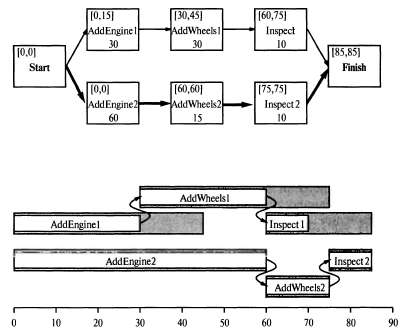

Рис. 12.1. Решение задачи планирования производства, приведенной в листинге 12.1. В верхней части этого рисунка решение показано в виде плана с частичным упорядочением. Продолжительность каждого действия обозначена в нижней части каждого прямоугольника, а значения самого раннего и самого позднего времени начала, условно обозначаемые как /"ES, LS], показаны в верхней левой части. Разность между этими двумя числами представляет собой резерв времени для действия; действия с нулевым резервом находятся на критическом пути, который обозначен жирными стрелками. В нижней части рисунка то же решение приведено в виде временного графика. Серые прямоугольники показывают интервалы времени, в течение которых может быть выполнено некоторое действие, при условии, что соблюдаются ограничения упорядочения. Незанятая часть серого прямоугольника обозначает резерв времени

Определив частичное упорядочение действий с учетом их продолжительности, как показано на рис. 12.1, можно применить метод критического пути (Critical Path Method — СРМ) для выяснения допустимых значений времени начала и окончания каждого действия. Путем через план с частичным упорядочением называется линейно упорядоченная последовательность действий, начинающаяся в состоянии Start и оканчивающаяся в состоянии Finish (например, в плане с частичным упорядочением, показанном на рис. 12.1, есть два пути).