|
Страница 4 из 4 Допустим, что Xi — переменная, для которой должна быть сформирована выборка, и предположим, что xi — все скрытые переменные, отличные от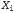 . Их значениями в текущем состоянии являются . Их значениями в текущем состоянии являются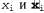 . Если будет выполнена выборка нового значения . Если будет выполнена выборка нового значения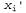 для переменной для переменной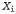 , обусловленного всеми прочими переменными, включая переменные свидетельства, то будет получено следующее: , обусловленного всеми прочими переменными, включая переменные свидетельства, то будет получено следующее: 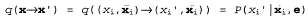
Это выражение для переходной вероятности называется формирователем выборок Гиббса (Gibbs sampler) и служит основой особенно удобной формы алгоритма МСМС. Теперь мы покажем, что формирователь выборок Гиббса находится в детализированном равновесии с истинной апостериорной вероятностью: 
Как указано на с. 1, переменная независима от всех других переменных, если дано ее марковское покрытие, поэтому имеет место следующее соотношение: 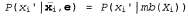
где mb(Xi) обозначает значения переменных в марковском покрытии Xi,, MB(Xi). Как показано в упр. 14.10, вероятность переменной, если дано ее марковское покрытие, пропорциональна вероятности переменной, если даны ее родительские переменные, умноженной на вероятность каждой дочерней переменной, если даны ее соответствующие родительские переменные: 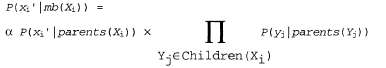 (14.11) (14.11)
Поэтому для изменения значения каждой переменной xi необходимо выполнить такое количество операций умножения, которое равно количеству дочерних переменных переменной xi. В этом разделе рассматривался только один простой вариант алгоритма МСМС — вариант, основанный на использовании формирователя выборок Гиббса. В своей наиболее общей форме алгоритм МСМС представляет собой мощный метод вычислений с помощью вероятностных моделей, поэтому было разработано много вариантов этого алгоритма, включая алгоритм эмуляции отжига (см. главу 4), алгоритмы стохастической выполнимости (см. главу 7) и формирователь выборок Мет-рополиса—Гастингса, рассматриваемый в главе 15.
<< В начало < Предыдущая 1 2 3 4 Следующая > В конец >>
|