|
Страница 3 из 4 Предположим, что — вероятность того, что в этом процессе произойдет переход из состояния χ в состояние x'. Эта переходная вероятность определяет информационную структуру, заданную на пространстве состояний, которая называется цепью Маркова. (Цепи Маркова играют также важную роль в главах 15 и 17.) Теперь предположим, что мы развернули цепь Маркова на t этапов, и допустим, что — вероятность того, что в этом процессе произойдет переход из состояния χ в состояние x'. Эта переходная вероятность определяет информационную структуру, заданную на пространстве состояний, которая называется цепью Маркова. (Цепи Маркова играют также важную роль в главах 15 и 17.) Теперь предположим, что мы развернули цепь Маркова на t этапов, и допустим, что — вероятность того, что система находится в состоянии χ во время t. Аналогичным образом, допустим, что — вероятность того, что система находится в состоянии χ во время t. Аналогичным образом, допустим, что — вероятность пребывания системы в состоянии x' во время t+1. Если дано значение — вероятность пребывания системы в состоянии x' во время t+1. Если дано значение , то значение , то значение можно рассчитать путем суммирования по всем состояниям, в которых система может находиться во время t, вероятностей пребывания в этом состоянии, умноженных на вероятности осуществления перехода в состояние x', следующим образом: можно рассчитать путем суммирования по всем состояниям, в которых система может находиться во время t, вероятностей пребывания в этом состоянии, умноженных на вероятности осуществления перехода в состояние x', следующим образом: 
Цепь называется достигшей своего стационарного распределения (stationary distribution), если . Назовем это стационарное распределение π; итак, его . Назовем это стационарное распределение π; итак, его определяющим уравнением является следующее: 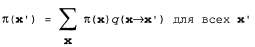 (14.9) (14.9)
При некоторых стандартных допущениях, касающихся распределения вероятностей перехода q, существует одно и только одно распределение π, удовлетворяющее этому уравнению при каждом конкретном значении q. Уравнение 14.9 можно трактовать как утверждение, что в установившемся режиме ожидаемый "отток" из каждого состояния (т.е. его текущее "население") равен ожидаемому "притоку" из всех других состояний. Один из очевидных способов удовлетворения этого отношения состоит в достижении того, чтобы ожидаемый поток между любыми парами состояний был одинаковым в обоих направлениях. В этом состоит свойство детализированного равновесия, которое показано ниже.  (14.10) (14.10)
Можно показать, что из этого свойства детализированного равновесия можно вывести свойство стационарности, получив суммы по x в уравнении 14.10. Получаем следующее соотношение: 
где возможен последний этап преобразования, поскольку гарантировано выполнение перехода из состояния x'. Теперь мы покажем, что вероятность перехода , определяемая на этапе формирования выборки в алгоритме MCMC-Ask, удовлетворяет уравнению детализированного равновесия со стационарным распределением, равным Р(х|е) (истинному апостериорному распределению по скрытым переменным). Мы проведем это доказательство в два этапа. Вначале определим цепь Маркова, в которой формирование выборки по каждой переменной обусловлено текущими значениями всех прочих переменных, и покажем, что это условие соответствует свойству детализированного равновесия. Затем мы просто констатируем, что для байесовских сетей формирование такой условной выборки эквивалентно условному формированию выборки по марковскому покрытию переменной (см. с. 1). , определяемая на этапе формирования выборки в алгоритме MCMC-Ask, удовлетворяет уравнению детализированного равновесия со стационарным распределением, равным Р(х|е) (истинному апостериорному распределению по скрытым переменным). Мы проведем это доказательство в два этапа. Вначале определим цепь Маркова, в которой формирование выборки по каждой переменной обусловлено текущими значениями всех прочих переменных, и покажем, что это условие соответствует свойству детализированного равновесия. Затем мы просто констатируем, что для байесовских сетей формирование такой условной выборки эквивалентно условному формированию выборки по марковскому покрытию переменной (см. с. 1).
|