Один из недостатков общих логических высказываний состоит в том, что может существовать много различных, логически эквивалентных высказываний, которые описывают одно и то же доверительное состояние, поэтому проверка повторяющихся состояний в алгоритме поиска в графе может потребовать применения средств общего доказательства теорем. По этой причине желательно было бы использовать для высказываний каноническое представление, в котором каждое доверительное состояние соответствует одному и только одному высказыванию. В одном из таких представлений используется конъюнкция литералов, упорядоченных по именам термов; в качестве примера можно привести. Такое представление можно рассматривать как стандартное представление состояния с учетом предположения об открытом мире, описанного в главе 11. Не все логические высказывания могут быть записаны в указанной форме (например, не существует способа представления высказывания), но такой метод представления доверительных состояний может применяться во многих проблемных областях.

3.    Высказывания с оценкой знаний, описывающие знания агента (см. также раздел 7.7). Для данного начального состояния такое высказывание имеет следующий вид:

где K обозначает "знает, что", а К(Р) указывает, что агент знает об истинности высказывания Р. В сочетании с высказываниями с оценкой знаний используется предположение о замкнутом мире — если высказывания с оценкой знаний нет в списке, оно рассматривается как ложное. Например, в приведенном выше высказывании неявно присутствуют термы и , поэтому оно представляет тот факт, что агент не знает истинностного значения терма CleanL.

Как оказалось, второй и третий из описанных выше вариантов являются приблизительно эквивалентными, но мы будем использовать третий вариант — высказывания с оценкой знаний, поскольку они позволяют получить более реалистичное описание процесса получения информации с помощью датчиков и поскольку нам уже известно, как составлять описания Strips при использовании предположения о замкнутом мире.

В обоих вариантах каждый пропозициональный символ может быть представлен в одном из трех видов: положительный, отрицательный или неизвестный. Поэтому существует точно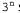возможных доверительных состояний, которые могут быть описаны таким образом. С другой стороны, множество доверительных состояний представляет собой показательное множество (множество всех подмножеств) множества физических состояний. Количество физических состояний равно, поэтому количество доверительных состояний равно, что намного превышает; это означает, что варианты 2 и 3 являются чрезвычайно ограниченными с точки зрения представления доверительных состояний. В настоящее время такая ситуация считается неизбежной, поскольку любая схема, способная представить любое возможное доверительное состояние, в наихудшем случае для представления каждого из них потребует битов. Наши простые схемы требуют только О(n) битов для представления каждого доверительного состояния, поэтому позволяют достичь компромисса, в котором выразительность принесена в жертву компактности. В частности, если происходит некоторое действие, одно из предусловий которого неизвестно, то результирующее доверительное состояние не будет точно представимым и результат действия также станет неизвестным.