|
Страница 1 из 2 При использовании единственной, дискретной переменной состояния можно определить более сжатую форму представлений модели перехода, модели восприятия, а также прямых и обратных сообщений. Предположим, что переменная состояния можно определить более сжатую форму представлений модели перехода, модели восприятия, а также прямых и обратных сообщений. Предположим, что переменная состояния имеет значения, обозначенные целыми числами имеет значения, обозначенные целыми числами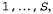 где S — количество возможных состояний. В таком случае модель перехода где S — количество возможных состояний. В таком случае модель перехода преобразуется в матрицу Τ с размерами S x S, где преобразуется в матрицу Τ с размерами S x S, где 
Таким образом, представляет собой вероятность перехода из состояния i в состояние j. Например, матрица перехода для мира задачи с зонтиком выглядит следующим образом: представляет собой вероятность перехода из состояния i в состояние j. Например, матрица перехода для мира задачи с зонтиком выглядит следующим образом: 
Переведем также в матричную форму модель восприятия. В данном случае, поскольку известно, что значение переменной свидетельства равно, скажем, равно, скажем, , необходимо использовать только ту часть модели, в которой определена вероятность появления значения , необходимо использовать только ту часть модели, в которой определена вероятность появления значения . Для каждого временного интервала t мы составим диагональную матрицу . Для каждого временного интервала t мы составим диагональную матрицу диагональные элементы которой задаются значениями диагональные элементы которой задаются значениями  , а остальные элементы равны 0. Например, в мире задачи с зонтиком в день 1 было получено значение , а остальные элементы равны 0. Например, в мире задачи с зонтиком в день 1 было получено значение , поэтому, согласно рис. 15.2, имеет место , поэтому, согласно рис. 15.2, имеет место
следующее: 
Теперь, если для представления прямых и обратных сообщений будут использоваться векторы столбцов, то все вычисления преобразуются в простые матрично-векторные операции. Прямое уравнение 15.3 принимает следующий вид:  (15.10) (15.10)
а обратное уравнение 15.7 становится следующим:  (15.11) (15.11)
Как показывают эти уравнения, временная сложность прямого—обратного алгоритма (см. листинг 15.1), применяемого к последовательности с длиной t, равна  , поскольку на каждом этапе требуется умножать вектор с S элементами на матрицу SxS. Потребность в пространстве измеряется величиной О (St), так как при проходе в прямом направлении необходимо сохранить в памяти t векторов с размером S. , поскольку на каждом этапе требуется умножать вектор с S элементами на матрицу SxS. Потребность в пространстве измеряется величиной О (St), так как при проходе в прямом направлении необходимо сохранить в памяти t векторов с размером S. Такая матричная формулировка не только становится изящным описанием алгоритмов фильтрации и сглаживания для моделей НММ, но и открывает возможности для создания улучшенных алгоритмов. Первым из таких алгоритмов является простой вариант прямого—обратного алгоритма, который обеспечивает выполнение сглаживания за счет использования постоянного пространства, независимо от длины последовательности. Идея этого алгоритма состоит в том, что для выполнения сглаживания в любом конкретном временном срезе к требуется одновременное присутствие в памяти и прямого, и обратного сообщений, , согласно уравнению 15.6. В прямом—обратном алгоритме это достигается за счет хранения значений f, вычисленных во время прохода в прямом направлении, для того, чтобы они были доступными во время прохода в обратном направлении. Еще один способ достижения этой цели состоит в использовании одного прохода, в котором и значение f, и значение b распространяются в одном и том же направлении. Например, можно добиться распространения "прямого" сообщения f в обратном направлении, преобразовав уравнение 15.10 таким образом, чтобы оно действовало в другом направлении, как показано ниже. , согласно уравнению 15.6. В прямом—обратном алгоритме это достигается за счет хранения значений f, вычисленных во время прохода в прямом направлении, для того, чтобы они были доступными во время прохода в обратном направлении. Еще один способ достижения этой цели состоит в использовании одного прохода, в котором и значение f, и значение b распространяются в одном и том же направлении. Например, можно добиться распространения "прямого" сообщения f в обратном направлении, преобразовав уравнение 15.10 таким образом, чтобы оно действовало в другом направлении, как показано ниже. 
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|