|
Страница 2 из 2 Этот модифицированный алгоритм сглаживания действует так, что в нем вначале осуществляется стандартный проход в прямом направлении для вычисления значения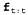 (при этом все промежуточные результаты уничтожаются), после чего выполняется проход в обратном направлении для совместного вычисления и b, и f, а затем эти значения используются для вычисления сглаженной оценки для каждого интервала. Поскольку требуется только одна копия каждого сообщения, потребности в памяти являются постоянными (т.е. независимыми от t, длины последовательности). Тем не менее этот алгоритм имеет одно существенное ограничение — в нем требуется, чтобы матрица перехода была обратимой, а модель восприятия не имела нулей, иными словами, чтобы каждое наблюдение было возможным в любом состоянии. (при этом все промежуточные результаты уничтожаются), после чего выполняется проход в обратном направлении для совместного вычисления и b, и f, а затем эти значения используются для вычисления сглаженной оценки для каждого интервала. Поскольку требуется только одна копия каждого сообщения, потребности в памяти являются постоянными (т.е. независимыми от t, длины последовательности). Тем не менее этот алгоритм имеет одно существенное ограничение — в нем требуется, чтобы матрица перехода была обратимой, а модель восприятия не имела нулей, иными словами, чтобы каждое наблюдение было возможным в любом состоянии. Матричная формулировка открывает возможности усовершенствования еще в одном направлении — в области создания методов оперативного сглаживания с постоянным запаздыванием. Тот факт, что сглаживание может быть выполнено за счет постоянных затрат пространства, наводит на мысль, что может существовать эффективный рекурсивный алгоритм для оперативного сглаживания, т.е. алгоритм, временная сложность которого остается независимой от величины запаздывания. Предположим, что запаздывание равно d; это означает, что сглаживание проводится во временном срезе t-d, притом что текущее время равно t. Согласно уравнению 15.6, для среза t-d необходимо рассчитать значение следующего выражения: 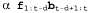
В таком случае после поступления новых результатов наблюдения необходимо будет вычислить следующее выражение для среза t-d+1: 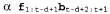
Как можно выполнить эту операцию инкрементно? Прежде всего, можно вычислить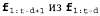 с использованием стандартного процесса фильтрации, в соответствии с уравнением 15.3. с использованием стандартного процесса фильтрации, в соответствии с уравнением 15.3. Инкрементное вычисление обратного сообщения является более сложным, поскольку не существует простого соотношения между старым обратным сообщением 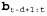 и новым обратным сообщением и новым обратным сообщением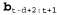 . Вместо этого рассмотрим соотношение между старым обратным сообщением . Вместо этого рассмотрим соотношение между старым обратным сообщением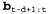 и обратным сообщением в начале последовательности, и обратным сообщением в начале последовательности,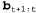 . Для этого d раз применим уравнение 15.11, чтобы получить следующее уравнение: . Для этого d раз применим уравнение 15.11, чтобы получить следующее уравнение: 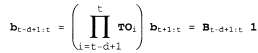 (15.12) (15.12)
где матрица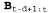 является произведением последовательности матриц О и т. является произведением последовательности матриц О и т. Матрицу в можно рассматривать как "оператор преобразования", который преобразует более позднее обратное сообщение в более раннее. Аналогичное уравнение остается справедливым для новых обратных сообщений, сформированных после поступления результатов следующего наблюдения: 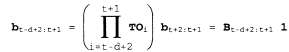 (15.13) (15.13)
Исследуя выражения для произведений в уравнениях 15.12 и 15.13, можно определить, что их связывает между собой простое соотношение, — чтобы получить второе произведение, достаточно "разделить" первое произведение на первый элемент 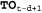 и умножить на новый последний элемент и умножить на новый последний элемент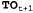 . Поэтому на языке алгебры матриц можно представить следующее простое соотношение между старой и новой матрицами в: . Поэтому на языке алгебры матриц можно представить следующее простое соотношение между старой и новой матрицами в: 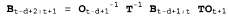 (15.14) (15.14)
Это уравнение предоставляет способ вычисления инкрементного обновления для матрицы в, которая, в свою очередь (в силу уравнения 15.13), позволяет вычислить новое обратное сообщение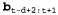 . Полный алгоритм, в котором предусматривается хранение и обновление значений f ив, показан в листинге 15.2. . Полный алгоритм, в котором предусматривается хранение и обновление значений f ив, показан в листинге 15.2. Листинг 15.2. Алгоритм сглаживания с постоянным временнь/м запаздыванием на d этапов, реализованный как оперативный алгоритм, который выводит новую сглаженную оценку после получения данных наблюдения, относящихся к новому временному интервалу 
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|