В данном разделе рассматриваются способы, позволяющие использовать для быстрого поиска решений структуру самой задачи, представленную в виде графа ограничений. Большинство описанных здесь подходов являются очень общими и применимыми для решения других задач, кроме CSP, например задач вероятностного формирования рассуждений. В конечном итоге единственный способ, с применением которого можно надеяться справиться с задачами реального мира, состоит в том, чтобы разложить их на множество подзадач. Еще раз обратившись к рис. 5.1, б с целью определить структуру задачи, можно обнаружить еще один факт: Тасмания не связана с материком. Интуитивно ясно, что задачи раскрашивания Тасмании и раскрашивания материка представляют собой независимые подзадачи — любое решение для материка, скомбинированное с любым решением для Тасмании, приводит к получению решения для всей карты. В том, что эти подзадачи являются независимыми, можно убедиться, рассматривая связные компоненты графа ограничений. Каждый компонент соответствует одной подзадаче CSPi. Если присваивание Si является решением CSPi, то является решением. Почему это так важно? Рассмотрим следующее: предположим, что каждая подзадача CSPi имеет с переменных из общего количества л переменных, где с — константа. В таком случае должно быть п/с подзадач, и для решения каждой из них требуется, самое большее, объем работы dc. 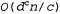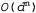Поэтому общий объем работы измеряется величиной, которая линейно зависит от л; без такой декомпозиции общий объем работы измерялся бы величиной, которая экспоненциально зависит от л. Приведем более конкретный пример: разделение булевой задачи CSP с c=80.на четыре подзадачи с с=20 сокращает продолжительность поиска решения в наихудшем случае от такой величины, которая равна сроку существования всей вселенной, до величины меньше одной секунды.

Поэтому полностью независимые подзадачи являются привлекательными, но встречаются редко. В большинстве случаев подзадачи любой задачи CSP связаны друг с другом. Простейшим случаем является тот, в котором граф ограничений образует дерево: любые две переменные связаны не больше чем одним путем. На рис. 5.6, а показан один из примеров в схематическом виде4. Ниже будет показано, что любая задана CSP с древовидной структурой может быть решена за время, линейно зависящее от количества переменных. Этот алгоритм имеет перечисленные ниже этапы.