Первый подход предусматривает присваивание значений некоторым переменным так, чтобы оставшиеся переменные образовывали дерево. Рассмотрим граф ограничений для карты Австралии, который еще раз показан на рис. 5.7, а. Если с этой карты можно было бы удалить узел SA, соответствующий Южной Австралии, то граф превратился бы в дерево, как показано на рис. 5.7, б. К счастью, это можно сделать (в графе, а не на самом континенте), зафиксировав некоторое значение для SA и удалив из областей определения других переменных все значения, несовместимые со значением, выбранным для SA.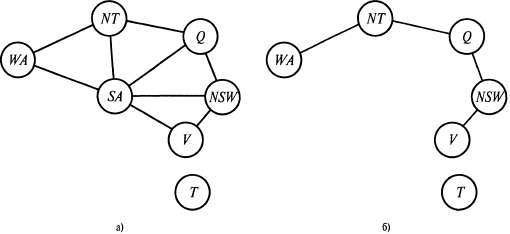

Рис. 5.7. Первый способ преобразования графа ограничений в дерево: первоначальный граф ограничений, впервые приведенный на рис. 5.1 (а); граф ограничений после удаления узла SA (б)

Теперь, после удаления узла SA и связанных с ним ограничений, любое решение данной задачи CSP будет совместимым со значением, выбранным для SA. (Такой способ удобен при решении бинарных задач CSP; при наличии ограничений более высокого порядка ситуация усложняется.) Поэтому появляется возможность решить задачу, представленную оставшимся деревом, с помощью приведенного выше алгоритма и таким образом решить всю проблему. Безусловно, в общем случае (в отличие от задачи раскрашивания карты) значение, выбранное для узла SA, может оказаться неподходящим, поэтому придется проверить каждое из возможных значений. Общий алгоритм решения указанным способом описан ниже.

•    Выбрать подмножество S из множества Variables [ csp], такое, что граф ограничений после удаления Остановится деревом. Подмножество S называется множеством разрыва цикла (cycle cutset).

•   Для каждого возможного присваивания переменным в 5, которое удовлетворяет всем ограничениям в 5, выполнить следующее:

•  удалить из областей определения оставшихся переменных любые значения, несовместимые с данным присваиванием для S;

•  если оставшаяся задача CSP имеет решение, вернуть это решение вместе с присваиванием для S.