|
Страница 5 из 5 Влияние такого компромисса можно наблюдать наиболее наглядно в случае использования логических гипотез, когда переменная Я содержит только детерминированные гипотезы. В таком случае значение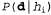 равно 1, если гипотезасо равно 1, если гипотезасо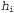 гласуется с данными, и 0 — в противном случае. Рассматривая уравнение 20.1, можно определить, что гласуется с данными, и 0 — в противном случае. Рассматривая уравнение 20.1, можно определить, что 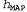 в таких условиях представляет собой простейшую логическую теорию, согласованную с данными. Поэтому обучение с помощью максимальной апостериорной гипотезы представляет собой естественное воплощение принципа бритвы Оккама. в таких условиях представляет собой простейшую логическую теорию, согласованную с данными. Поэтому обучение с помощью максимальной апостериорной гипотезы представляет собой естественное воплощение принципа бритвы Оккама. Еще один способ анализа компромисса между сложностью и степенью согласованности состоит в том, что можно исследовать уравнение 20.1, взяв его логарифм. Применение значения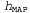 для максимизации выражения для максимизации выражения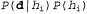 эквивалентно минимизации следующего выражения: эквивалентно минимизации следующего выражения: 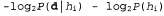
Используя связь между информационным содержанием и вероятностью, которая была описана в главе 18, можно определить, что терм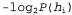 определяет количество битов, требуемых для задания гипотезы определяет количество битов, требуемых для задания гипотезы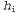 . Кроме того, терм . Кроме того, терм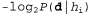 представляет собой дополнительное количество битов, требуемых для задания данных, если дана рассматриваемая гипотеза (чтобы убедиться в этом, достаточно отметить, что если гипотеза точно предсказывает данные, как в случае гипотезы представляет собой дополнительное количество битов, требуемых для задания данных, если дана рассматриваемая гипотеза (чтобы убедиться в этом, достаточно отметить, что если гипотеза точно предсказывает данные, как в случае гипотезы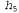 и сплошного ряда конфет с лимонными леденцами, не требуется ни одного бита, поскольку и сплошного ряда конфет с лимонными леденцами, не требуется ни одного бита, поскольку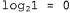 ). Таким образом, обучение с помощью МАР-гипотезы равносильно выбору гипотезы, которая обеспечивает максимальное сжатие данных. Такую же задачу можно решить более прямо с помощью метода обучения на основе минимальной длины описания, или сокращенно MDL (Minimum Description ). Таким образом, обучение с помощью МАР-гипотезы равносильно выбору гипотезы, которая обеспечивает максимальное сжатие данных. Такую же задачу можно решить более прямо с помощью метода обучения на основе минимальной длины описания, или сокращенно MDL (Minimum Description Length), в котором вместо манипуляций с вероятностями предпринимаются попытки минимизировать размер гипотезы и закодированного представления данных. Окончательное упрощение может быть достигнуто путем принятия предположения о равномерном распределении априорных вероятностей по пространству гипотез. В этом случае обучение с помощью МАР-гипотезы сводится в выбору гипотезы 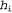 , которая максимизирует значение , которая максимизирует значение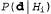 . Такая гипотеза называется гипотезой с максимальным правдоподобием (Maximum Likelihood — ML) и сокращенно обозначается . Такая гипотеза называется гипотезой с максимальным правдоподобием (Maximum Likelihood — ML) и сокращенно обозначается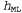 . Обучение на основе гипотезы с максимальным правдоподобием очень широко применяется в статистике, поскольку в этой научной области многие исследователи не доверяют распределениям априорных вероятностей гипотезы, считая, что они имеют субъективный характер. Это — приемлемый подход, применяемый в тех обстоятельствах, когда нет оснований априорно отдавать предпочтение одной гипотезе перед другой, например, в тех условиях, когда все гипотезы являются в равной степени сложными. Такой метод обучения становится хорошей аппроксимацией байесовского обучения и обучения с помощью МАР-гипотезы, когда набор данных имеет большие размеры, поскольку данные сами исправляют распределение априорных вероятностей по гипотезам, но связан с возникновением определенных проблем (как будет показано ниже) при использовании небольших наборов данных. . Обучение на основе гипотезы с максимальным правдоподобием очень широко применяется в статистике, поскольку в этой научной области многие исследователи не доверяют распределениям априорных вероятностей гипотезы, считая, что они имеют субъективный характер. Это — приемлемый подход, применяемый в тех обстоятельствах, когда нет оснований априорно отдавать предпочтение одной гипотезе перед другой, например, в тех условиях, когда все гипотезы являются в равной степени сложными. Такой метод обучения становится хорошей аппроксимацией байесовского обучения и обучения с помощью МАР-гипотезы, когда набор данных имеет большие размеры, поскольку данные сами исправляют распределение априорных вероятностей по гипотезам, но связан с возникновением определенных проблем (как будет показано ниже) при использовании небольших наборов данных.
<< В начало < Предыдущая 1 2 3 4 5 Следующая > В конец >>
|