В книге Port-Royal Logic ("Логика Пор-Ройяль"), написанной в 1662 году, французский философ Арно изложил следующую мысль.

"Чтобы судить о том, что следует делать, чтобы получить хорошее или избежать плохого, необходимо рассматривать не только хорошее и плохое само по себе, но и вероятность того, произойдет ли оно или не произойдет, а также рассматривать математически пропорцию, в которой все эти обстоятельства встречаются вместе."

В современной литературе вместо понятий хорошего или плохого применяется понятие полезности, но общий принцип остается таким же. Для описания предпочтений агента, с помощью которых он различает состояния мира, применяется функция полезности, которая присваивает состоянию единственное числовое значение, чтобы показать, насколько оно желательно. Полезности объединяются с вероятностями действий для определения ожидаемой полезности каждого действия.

В этой главе будет использоваться запись U(S) для обозначения полезности состояния S с точки зрения агента, принимающего решения. На данный момент мы будем рассматривать состояния как полные снимки параметров мира, по аналогии с ситуациями, которые рассматривались в главе 10. На первых порах такой подход позволяет упростить изложение данной темы, но когда придется отдельно определять полезность каждого возможного состояния, он может стать довольно громоздким. В разделе 16.4 будет показано, как можно выполнить в некоторых обстоятельствах декомпозицию состояний в целях присваивания значений полезности.

Любое недетерминированное действие А имеет возможные результирующие состояния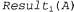, где индекс i пробегает по различным результатам. Прежде чем осуществить действие А, агент присваивает вероятность каждому результату, где Ε представляет собой сумму доступных агенту свидетельств о мире, a Do (А) — высказывание, согласно которому действие А выполняется в текущем состоянии. Таким образом, можно вычислить ожидаемую полезность действия с учетом свидетельства, EU( A| Ε), с использованием следующей формулы:

(16.1)