|
Страница 2 из 4 По-видимому, одним из наиболее широко применяемых методов решения задачи SLAM является EKF. Обычно этот метод используется в сочетании с моделью восприятия данных об отметках и требует, чтобы все отметки были различимыми. В предыдущем разделе апостериорная оценка была представлена с помощью гауссова распределения со средним и ковариацией и ковариацией . При использовании для решения задачи SLAM подхода, основанного на методе EKF, это распределение апостериорных вероятностей снова становится гауссовым, но теперь среднее . При использовании для решения задачи SLAM подхода, основанного на методе EKF, это распределение апостериорных вероятностей снова становится гауссовым, но теперь среднее выражается в виде вектора с гораздо большим количеством измерений. В нем представлена не только поза робота, но и местонахождение всех характеристик (или отметок) на карте. Если количество таких характеристик равно л, то вектор будет иметь размерность 2 n+3 (два значения требуются для указания местонахождения отметки и три — для указания позы робота). Следовательно, матрица выражается в виде вектора с гораздо большим количеством измерений. В нем представлена не только поза робота, но и местонахождение всех характеристик (или отметок) на карте. Если количество таких характеристик равно л, то вектор будет иметь размерность 2 n+3 (два значения требуются для указания местонахождения отметки и три — для указания позы робота). Следовательно, матрица имеет размерность (2 n+3) x(2 n+3) и следующую структуру: имеет размерность (2 n+3) x(2 n+3) и следующую структуру: 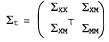 (25.2) (25.2)
В этом уравнении — ковариация данных о позе робота, которая уже рассматривалась в контексте локализации; — ковариация данных о позе робота, которая уже рассматривалась в контексте локализации;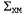 — матрица с размерами 3x2n, которая выражает корреляцию между характеристиками на карте и координатами робота. Наконец, — матрица с размерами 3x2n, которая выражает корреляцию между характеристиками на карте и координатами робота. Наконец, — это матрица с размерами 2лх2л, которая задает ковариацию характеристик на карте, включая все парные корреляции. Поэтому потребность в памяти для алгоритмов, основанных на методе EKF, измеряется квадратичной зависимостью от л (количества характеристик на карте), а время обновления также определяется квадратичной зависимостью от л. — это матрица с размерами 2лх2л, которая задает ковариацию характеристик на карте, включая все парные корреляции. Поэтому потребность в памяти для алгоритмов, основанных на методе EKF, измеряется квадратичной зависимостью от л (количества характеристик на карте), а время обновления также определяется квадратичной зависимостью от л. Прежде чем перейти к изучению математических выкладок, рассмотрим решение задачи по методу EKF на графиках. На рис. 25.10 показано, как робот движется в среде с восемью отметками, расположенными в два ряда по четыре отметки каждый. Первоначально робот не имеет информации о том, где находятся отметки. Предполагается, что каждая отметка имеет другой цвет, и робот может надежно отличать их друг от друга. Робот начинает двигаться влево, в заранее заданном направлении, но постепенно теряет уверенность в том, есть ли у него достоверная информация о своем местонахождении. Эта ситуация показана на рис. 25.10, а с помощью эллипсов погрешности, ширина которых возрастает по мере дальнейшего передвижения робота. Движущийся робот получает данные о дальности и азимуте до ближайших отметок, а эти наблюдения используются для получения оценок местонахождения таких отметок. Естественно, что неопределенность в оценке местонахождения этих отметок тесно связана с неопределенностью локализации робота. На рис. 25.10, б, в показано изменение доверительного состояния робота по мере того, как он продвигается в своей среде все дальше и дальше.
|