|
Страница 2 из 2 Аналогичные модели могут быть составлены для каждого слова, которое мы хотим распознать. Модель для фонемы с тремя состояниями показана в виде диаграммы перехода между состояниями на рис. 15.16. Эта модель относится только к одной конкретной фонеме, [т], но все фонемы должны иметь модели с аналогичной топологией. Для каждого состояния фонемы показана связанная с ней акустическая модель, в которой принято предположение, что соответствующий акустический сигнал представлен меткой VQ. Например, согласно этой модели, Обратите внимание на то, что на данном рисунке показаны петли; например, состояние Обратите внимание на то, что на данном рисунке показаны петли; например, состояние 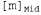 сохраняется с вероятностью 0.9, а это означает, что состояние сохраняется с вероятностью 0.9, а это означает, что состояние 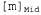 имеет ожидаемую продолжительность 10 фреймов. В рассматриваемой модели продолжительность каждой фонемы является независимой от продолжительности других фонем; в более сложной модели могут проводиться различия между быстрой и медленной речью. имеет ожидаемую продолжительность 10 фреймов. В рассматриваемой модели продолжительность каждой фонемы является независимой от продолжительности других фонем; в более сложной модели могут проводиться различия между быстрой и медленной речью. 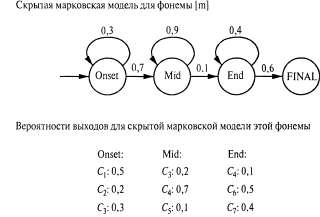 Рис. 15.16. Скрытая марковская модель для фонемы [т] с тремя состояниями. Каждое состояние имеет несколько возможных выходов, каждый из которых обладает собственной вероятностью. Метки 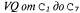 выбраны произвольно, в качестве примера выбраны произвольно, в качестве примера Аналогичные модели можно составить для каждой фонемы, возможно, с учетом трехфонемного контекста. Модель каждого слова, в сочетании с моделями его фонем, задает полную спецификацию некоторой скрытой марковской модели, которая, в свою очередь, определяет вероятности перехода между состояниями фонем от фрейма к фрейму, а также вероятности акустических характеристик для каждого состояния фонем. Если требуется распознавать отдельные слова (т.е. слова, произнесенные без какого-либо окружающего контекста и с четкими границами), то необходимо найти слово, которое максимизирует следующее выражение: 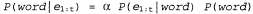
Априорную вероятность Ρ (word) можно получить по результатам обработки фактических речевых данных, а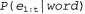 представляет собой правдоподобие последовательности акустических характеристик, соответствующих модели рассматриваемого слова word. Вопросу о том, как вычисляются такие значения правдоподобия, посвящен раздел 15.2; в частности, в уравнении 15.5 определен простой метод рекурсивного вычисления, стоимость которого линейно зависит от t и от количества состояний марковской цепи. Чтобы найти наиболее вероятное слово, можно выполнить это вычисление для каждой возможной модели слова, умножить полученное значение на априорную вероятность и в соответствии с этим выбрать наиболее подходящее слово. представляет собой правдоподобие последовательности акустических характеристик, соответствующих модели рассматриваемого слова word. Вопросу о том, как вычисляются такие значения правдоподобия, посвящен раздел 15.2; в частности, в уравнении 15.5 определен простой метод рекурсивного вычисления, стоимость которого линейно зависит от t и от количества состояний марковской цепи. Чтобы найти наиболее вероятное слово, можно выполнить это вычисление для каждой возможной модели слова, умножить полученное значение на априорную вероятность и в соответствии с этим выбрать наиболее подходящее слово.
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|