|
Страница 2 из 3 Более эффективный подход состоит в создании системы поддержки истинности на основе обоснований, или системы JTMS (Justification-Based Truth Maintenance System). В системе JTMS к каждому высказыванию в базе знаний прилагается аннотация в виде обоснования, состоящего из множества высказываний, на основании которых было выведено это высказывание. Например, если база знаний уже содержит высказывание то операция Tell (Р) вызовет добавление Q с обоснованием то операция Tell (Р) вызовет добавление Q с обоснованием 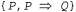 . Вообще говоря, высказывание может иметь любое количество обоснований. Обоснования используются для обеспечения эффективного извлечения. После выполнения вызова Retract (P) система JTMS удалит такие и только такие высказывания, для которых Ρ является элементом каждого обоснования. Поэтому, если высказывание Q имеет единственное обоснование . Вообще говоря, высказывание может иметь любое количество обоснований. Обоснования используются для обеспечения эффективного извлечения. После выполнения вызова Retract (P) система JTMS удалит такие и только такие высказывания, для которых Ρ является элементом каждого обоснования. Поэтому, если высказывание Q имеет единственное обоснование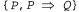 , оно будет удалено; если имеет также дополнительное обоснование , оно будет удалено; если имеет также дополнительное обоснование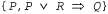 , оно также будет удалено; но если, кроме этого, имеет обоснование , оно также будет удалено; но если, кроме этого, имеет обоснование 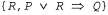 , оно будет сохранено. Таким образом, время, требуемое для извлечения высказывания Р, зависит только от количества высказываний, полученных на основании Р, а не от количества других высказываний, добавленных после того, как Ρ было введено в базу знаний. , оно будет сохранено. Таким образом, время, требуемое для извлечения высказывания Р, зависит только от количества высказываний, полученных на основании Р, а не от количества других высказываний, добавленных после того, как Ρ было введено в базу знаний. В системе JTMS предполагается, что высказывания, которые уже когда-то рассматривались, по-видимому, будут рассматриваться снова, поэтому вместо полного удаления из базы знаний некоторого высказывания после того, как оно теряет все обоснования, это высказывание просто отмечается как находящееся вне базы знаний. Если же какое-то последующее утверждение восстанавливает одно из обоснований, то это высказывание снова отмечается как находящееся внутри базы. Благодаря этому система JTMS позволяет сохранить все цепочки логического вывода, которые в ней используются, и не нуждается в повторном выводе высказываний после того, как некоторое обоснование вновь становится действительным. Кроме успешного исключения из базы знаний неправильной информации, системы поддержки истинности могут также использоваться для ускорения анализа многочисленных гипотетических ситуаций. Предположим, например, что Олимпийский комитет Румынии выбирает площадки для проведения соревнований по плаванию, легкой атлетике и конному спорту для олимпийских игр 2048 года, которые должны проводиться в Румынии. Например, допустим, что первой гипотезой является следующая: Site {Swimming, Pi testi), Site {Athletics, Bucharest) и Site {Equestrian, Arad). В таком случае необходимо провести большой объем рассуждений, чтобы определить логические следствия, а значит и целесообразность этого выбора. Если же вместо этого потребуется рассмотреть вариант Site{Athletics, Sibiu), то такая система TMS позволит избавиться от необходимости начинать всю эту работу с нуля. Вместо этого достаточно будет просто извлечь гипотезу Site {Athletics, Bucharest) и ввести Site {Athletics, Sibiu), после чего система TMS возьмет на себя весь необходимый пересмотр. А цепочки логического вывода, выработанные на основании выбора площадки в Бухаресте, могут повторно использоваться для Сибиу, при условии, что логические заключения остаются теми же самыми.
|