|
Страница 2 из 4 При использовании этого определения "расстояние" между двумя векторами, 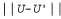 , представляет собой максимальную разность между двумя соответствующими элементами. Основным математическим результатом данного раздела является такое утверждение: допустим, что , представляет собой максимальную разность между двумя соответствующими элементами. Основным математическим результатом данного раздела является такое утверждение: допустим, что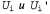 — два вектора полезностей. В таком случае получим следующее: — два вектора полезностей. В таком случае получим следующее: 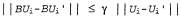 (17.7) (17.7)
Это означает, что обновление Беллмана представляет собой функцию сжатия на коэффициент у, применяемую к пространству векторов полезностей. Таким образом, процедура итерации по значениям всегда сходится к уникальному решению уравнений Беллмана. В частности, можно заменить значение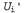 в уравнении 17.7 истинными полезностя-ми U, для которых BU=U. В таком случае будет получено следующее неравенство: в уравнении 17.7 истинными полезностя-ми U, для которых BU=U. В таком случае будет получено следующее неравенство: 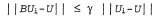
Поэтому, если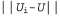 рассматривается как ошибка в оценке рассматривается как ошибка в оценке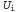 , то можно видеть, что эта ошибка уменьшается при каждой итерации на коэффициент, по меньшей мере равный γ. Это означает, что процедура итерации по значениям сходится экспоненциально быстро. Можно легко рассчитать количество итераций, требуемых для достижения заданной предельной ошибки ε, как описано ниже. Вначале напомним, что, как показывает уравнение 17.1, полезности всех состояний ограничены значением , то можно видеть, что эта ошибка уменьшается при каждой итерации на коэффициент, по меньшей мере равный γ. Это означает, что процедура итерации по значениям сходится экспоненциально быстро. Можно легко рассчитать количество итераций, требуемых для достижения заданной предельной ошибки ε, как описано ниже. Вначале напомним, что, как показывает уравнение 17.1, полезности всех состояний ограничены значением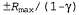 . Из этого следует, что максимальная начальная ошибка определяется соотношением . Из этого следует, что максимальная начальная ошибка определяется соотношением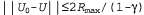 . Предположим, что для достижения ошибки, не превышающей ε, выполнено N итераций. В таком случае потребуется . Предположим, что для достижения ошибки, не превышающей ε, выполнено N итераций. В таком случае потребуется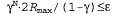 итераций, поскольку ошибка уменьшается каждый раз по меньшей мере на величину γ. Взяв логарифмы от этого выражения, можно определить, что достаточно применить следующее количество итераций: итераций, поскольку ошибка уменьшается каждый раз по меньшей мере на величину γ. Взяв логарифмы от этого выражения, можно определить, что достаточно применить следующее количество итераций: 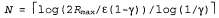
|