|
Страница 2 из 3 Но не все правила логического вывода действуют в обоих направлениях, как это. Например, нельзя применить правило отделения в противоположном направлении, чтобы получить высказывания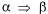 и α из высказывания β. и α из высказывания β. Рассмотрим, как можно использовать эти правила логического вывода и эквивалентности в мире вампуса. Начнем с базы знаний, содержащей высказывания , и покажем, как доказать высказывание , и покажем, как доказать высказывание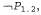 т.е. утверждение, что в квадрате [1,2] нет ямы. Вначале применим правило удаления двухсторонней импликации к высказыванию т.е. утверждение, что в квадрате [1,2] нет ямы. Вначале применим правило удаления двухсторонней импликации к высказыванию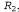 , чтобы получить следующее: , чтобы получить следующее: 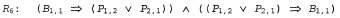
Затем применим к высказыванию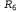 правило удаления связки "И" и получим: правило удаления связки "И" и получим: 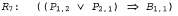
Из логической эквивалентности отрицаний следует: 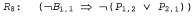
Теперь можно применить правило отделения к высказыванию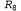 и к высказыванию и к высказыванию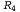 с данными восприятия (т.е. с данными восприятия (т.е.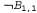 ), чтобы получить следующее: ), чтобы получить следующее: 
Наконец, применим правило де Моргана, позволяющее получить такое заключение: 
Это означает, что ни в квадрате [ 1, 2 ], ни в квадрате [2,1] нет ямы. Приведенный выше процесс логического вывода (последовательность применения правил логического вывода) называется доказательством. Процесс формирования доказательств полностью аналогичен процессу обнаружения решений в задачах поиска. В действительности, если можно было бы составить функцию определения преемника для выработки всех возможных вариантов применения правил логического вывода, это позволило бы использовать для формирования доказательств все алгоритмы поиска, приведенные в главах 3 и 4. Таким образом, вместо трудоемкого перебора моделей может применяться более эффективный способ логического вывода — формирование доказательств. Поиск может проходить в прямом направлении, от первоначальной базы знаний, и осуществляться путем использования правил логического вывода для получения целевого высказывания, или же этот поиск может проходить в обратном направлении, от целевого высказывания, в попытке найти цепочку правил логического вывода, ведущую от первоначальной базы знаний. Ниже в этом разделе рассматриваются два семейства алгоритмов, в которых используются оба эти подхода.
|