|
Страница 1 из 3 Как было указано выше, сглаживание — это процесс вычисления распределения вероятностей значений переменных в прошлых состояниях при наличии свидетельств вплоть до нынешнего состояния, иными словами, для для  (рис. 15.3.) Такие вычисления наиболее удобно разбить на две части: применительно к свидетельствам вплоть до момента времени k и к свидетельствам от к+1 до t: (рис. 15.3.) Такие вычисления наиболее удобно разбить на две части: применительно к свидетельствам вплоть до момента времени k и к свидетельствам от к+1 до t: 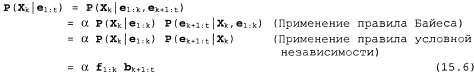
где используется сообщение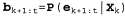 , определяемое как "обратное", по аналогии с прямым сообщением , определяемое как "обратное", по аналогии с прямым сообщением . Прямое сообщение . Прямое сообщение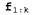 может быть вычислено путем фильтрации в прямом направлении от 1 до к в соответствии с уравнением 15.3. Как оказалось, обратное сообщение может быть вычислено путем фильтрации в прямом направлении от 1 до к в соответствии с уравнением 15.3. Как оказалось, обратное сообщение может быть вычислено с помощью рекурсивного процесса, который осуществляется в обратном направлении от t: может быть вычислено с помощью рекурсивного процесса, который осуществляется в обратном направлении от t: 
где последний этап преобразования следует из свойства условной независимости 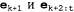 , если дано , если дано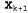 . Из трех множителей в этой операции суммирования первый и третий можно получить непосредственно с помощью модели, а второй представляет собой "рекурсивный вызов". С использованием обозначения для сообщений получим следующее: . Из трех множителей в этой операции суммирования первый и третий можно получить непосредственно с помощью модели, а второй представляет собой "рекурсивный вызов". С использованием обозначения для сообщений получим следующее: 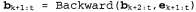
где функция Backward осуществляет обновление, описанное в уравнении 15.7. Как и при рекурсии в прямом направлении, время и пространство, требуемые для каждого обновления, являются постоянными и поэтому независимыми от t. 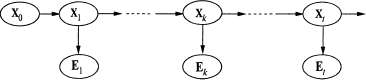 Рис. 15.3. Процесс сглаживания, в котором вычисляется , распределение апостериорных вероятностей значений переменных в состоянии, наблюдавшемся в какой-то прошлый момент времени к, если дана полная последовательность наблюдений от ldot , распределение апостериорных вероятностей значений переменных в состоянии, наблюдавшемся в какой-то прошлый момент времени к, если дана полная последовательность наблюдений от ldot Теперь становится вполне очевидно, что оба терма, приведенные в уравнении 15.6, можно вычислить с помощью рекурсий по времени, одна из которых проходит в прямом направлении от 1 до к и в которой используется уравнение фильтрации 15.3, а другая проходит в обратном направлении от t до к+1 и в ней используется уравнение 15.7. Следует отметить, что этап обратной рекурсии инициализируется с помощью выражения , где 1 — вектор из единиц (поскольку , где 1 — вектор из единиц (поскольку 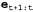 — пустая последовательность, вероятность наблюдения равна 1). — пустая последовательность, вероятность наблюдения равна 1).
Итак, применим этот алгоритм к примеру с зонтиком и вычислим сглаженную оценку вероятности дождя в момент времени t=l по данным наблюдений за появлением директора с зонтиком в дни 1 и 2. Согласно уравнению 15.6, это значение определяется следующим образом:  (15.8) (15.8)
<< В начало < Предыдущая 1 2 3 Следующая > В конец >>
|