Как нам уже известно, первый терм равен <. 818, . 182>, согласно результатам применения процесса прямой фильтрации, описанного выше. Второй терм можно вычислить, применив обратную рекурсию по уравнению 15.7:

Подставляя эти значения в уравнение 15.8, можно найти, что сглаженная оценка вероятности дождя в день 1 такова:

Таким образом, в данном случае сглаженная оценка выше, чем отфильтрованная оценка (0 .818). Это связано с тем, что появление директора с зонтиком в день 2 повышает вероятность того, что в день 2 шел дождь; в свою очередь, поскольку дожди обычно являются затяжными, это приводит к повышению вероятности дождя и в день 1.

И для прямой, и для обратной рекурсии требуется постоянное количество времени в расчете на каждый этап; поэтому временная сложность сглаживания по отношению к свидетельству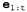составляет О (t). Этим выражением определяется также сложность сглаживания в конкретном интервале времени к. А если требуется провести сглаживание всей последовательности, то один из очевидных методов состоит в выполнении всего процесса сглаживания по одному разу для каждого интервала времени, в котором должно быть выполнено сглаживание. Такой подход приводит к получению временной сложности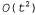. Но в лучшем подходе можно было бы использовать очень простое приложение динамического программирования, чтобы свести сложность к величине 0{t). Один из намеков на то, как это сделать, можно найти в приведенном выше анализе примера с зонтиком, где была показана возможность повторного использования результатов прямой фильтрации. Ключом к созданию алгоритма с линейными затратами времени является регистрация результатов прямой фильтрации по всей последовательности. В таком случае можно выполнить обратную рекурсию от t вплоть до 1, вычисляя сглаженную оценку для каждого этапа к из вычисленного обратного сообщенияи хранимого прямого сообщения . 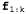Этот алгоритм, обоснованно названный прямым—обратным алгоритмом (forward—backward algorithm), показан в листинге 15.1.

Листинг 15.1. Прямой—обратный алгоритм для вычисления апостериорных вероятностей последовательности состояний при наличии последовательности наблюдений. Операторы Forward и Backward определены в уравнениях 15.3 и 15.7

Внимательный читатель должен был заметить, что структура байесовской сети, показанной на рис. 15.3, представляет собой полидерево, согласно терминологии главы 14. Это означает, что непосредственное применение алгоритма кластеризации также приводит к созданию алгоритма с линейными затратами времени, который вычисляет сглаженные оценки для всей последовательности. Итак, вполне понятно, что прямой—обратный алгоритм фактически представляет собой частный случай алгоритма распространения в полидереве, используемого в сочетании с методами кластеризации (хотя эти два алгоритма были разработаны независимо).