|
Страница 2 из 3 Эти правила позволяют свести задачу определения истинности сложных высказываний к задаче определения истинности более простых высказываний. Правила определения истинности для каждой связки могут быть подытожены в виде ^ истинностной таблицы, которая определяет истинностное значение сложного высказывания для каждого возможного присваивания значений истинности его компонентам. Истинностные таблицы для рассматриваемых пяти логических связок приведены в табл. 7.1. С использованием этих таблиц истинностное значение любого высказывания s применительно к любой модели т может быть вычислено с помощью простого процесса рекурсивной оценки. Например, высказывание 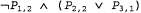 , оцениваемое в модели ml9 приводит к получению , оцениваемое в модели ml9 приводит к получению 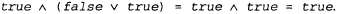 В упр. 7.3 предложено написать алгоритм PL-True? (s,т), который вычисляет истинностное значение любого высказывания s пропозициональной логики в модели т. В упр. 7.3 предложено написать алгоритм PL-True? (s,т), который вычисляет истинностное значение любого высказывания s пропозициональной логики в модели т. Выше было сказано, что любая база знаний состоит из множества высказываний. Теперь можно показать, что логическая база знаний представляет собой конъюнкцию этих высказываний. Это означает, что, начиная с пустой базы знаний кв и применяя операции , мы получим: , мы получим: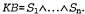 Таким образом, базы знаний и высказывания могут рассматриваться как взаимозаменяемые понятия. Таблица 7.1. Истинностные таблицы для пяти логических связок. Чтобы воспользоваться этой таблицей, например для вычисления значения Р v Q, когда Р является истинным, a Q — ложным, вначале необходимо найти в левой части таблицы строку, в которой Р имеет значение true, a Q — false (третья строка). Затем нужно искать запись в этой строке, соответствующую столбцу Р v Q, чтобы определить результат — true. Еще один способ поиска истинностного значения состоит в том, что каждая строка может рассматриваться как модель, а записи под каждым столбцом для этой строки — как утверждение о том, является ли соответствующее высказывание истинным в данной модели  Истинностные таблицы для связок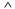 ("и"), ("и"),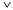 ("или") и ("или") и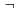 ("нет") почти полностью соответствуют интуитивным представлениям о смысле таких же слов естественного языка. Основным источником возможной путаницы является то, что высказывание Р v Q истинно, если истинными являются Р, или Q, или оба эти высказывания. Есть также другая связка, называемая "исключительное ИЛИ" (сокращенно "XOR" — exclusive OR), которая принимает ложное значение, если оба дизъюнкта являются истинными9. В отношении того, какое обозначение следует применять для связки "исключительное ИЛИ", нет общего согласия; двумя возможными вариантами являются ("нет") почти полностью соответствуют интуитивным представлениям о смысле таких же слов естественного языка. Основным источником возможной путаницы является то, что высказывание Р v Q истинно, если истинными являются Р, или Q, или оба эти высказывания. Есть также другая связка, называемая "исключительное ИЛИ" (сокращенно "XOR" — exclusive OR), которая принимает ложное значение, если оба дизъюнкта являются истинными9. В отношении того, какое обозначение следует применять для связки "исключительное ИЛИ", нет общего согласия; двумя возможными вариантами являются
|