|
Страница 1 из 4 В 1909 году Чарльз Пирс предложил графическую систему обозначений в виде узлов и дуг, получившую название экзистенциальных графов, которую он назвал "логикой будущего". Так зародилось понятие семантических сетей. С того времени и начались продолжительные дебаты между приверженцами "чистой логики" и приверженцами "чисто семантических сетей". К сожалению, эти дебаты затмили тот факт, что семантические сети (по меньшей мере, те из них, в которых правильно определена семантика) представляют собой всего лишь одну из форм логики. Система обозначений для высказываний некоторых типов, предусмотренная в семантических сетях, часто является более удобной для человека, но если отбросить эти особенности, касающиеся "удобного интерфейса", то базовые понятия (объекты, отношения, кванторы и т.д.) окажутся теми же самыми. Существует много вариантов семантических сетей, но все они способны представлять отдельные объекты, категории объектов и отношения между объектами. В типичной графической системе обозначений имена объектов или категорий изображаются в овалах или прямоугольниках, а связи между ними обозначаются с помощью дуг с метками. Например, на рис. 10.7 показана связь MemberOf между Маrу и FemalePersons, которая соответствует логическому утверждению Mary e FemalePersons; аналогичным образом, связь SisterOf между Магу и John соответствует утверждению SisterOf (Mary, John). Категории можно соединять с помощью связи SubsetOf и т.д. Рисовать эти овалы и стрелки так интересно, что часто можно забыть обо всем. Например, мы знаем, что матерями людей являются особы женского пола, но можно ли нарисовать связь HasMother от категории Persons к категории FemalePersons! Ответ является отрицательным, поскольку HasMother— это связь между человеком и его матерью, а категории не имеют матерей7. По этой причине на рис. 10.7 используется специальное обозначение — связь с меткой в прямоугольнике с двойным контуром. Эта связь соответствует следующему утверждению: 
Нам может также потребоваться сформулировать утверждение, что люди имеют две ноги, таким образом: 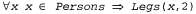
<< В начало < Предыдущая 1 2 3 4 Следующая > В конец >>
|