|
Страница 1 из 6 Выше было показано, что все рассматривавшиеся до сих пор правила логического вывода являются непротиворечивыми, но вопрос об их полноте применительно к алгоритмам логического вывода, в которых они используются, еще не обсуждался. Алгоритмы поиска, такие как поиск с итеративным углублением (с. 133), являются полными в том смысле, что позволяют найти любую достижимую цель, но если доступные правила логического вывода неадекватны, то цель становится недостижимой; это означает, что не существует доказательства, в котором могли бы применяться только эти правила логического вывода. Например, если мы откажемся от использования правила удаления двухсторонней импликации, то не сможем довести до конца доказательство, изложенное в предыдущем разделе. А в настоящем разделе представлено единственное правило логического вывода, правило резолюции, позволяющее получить алгоритм логического вывода, который становится полным в сочетании с любым полным алгоритмом поиска. Начнем с использования простой версии правила резолюции в мире вампуса. Рассмотрим шаги, ведущие вверх на рис. 7.3, а: агент возвращается из квадрата [2,1] в квадрат [ 1,1 ], а затем переходит в квадрат [ 1, 2 ], где он чувствует неприятный запах, но не ощущает ветерка. Введем следующие дополнительные факты в базу знаний: 
С помощью того же процесса, который привел к получению высказывания приведенного выше, мы теперь можем сделать заключение об отсутствии ям в квадратах [2,2] и [1,3] (напомним, что в отношении квадрата [1,1] уже известно, что в нем нетям): приведенного выше, мы теперь можем сделать заключение об отсутствии ям в квадратах [2,2] и [1,3] (напомним, что в отношении квадрата [1,1] уже известно, что в нем нетям): 
Кроме того, можно применить к высказыванию правило удаления двухсторонней импликации, после чего применить к полученному результату в сочетании с высказыванием R5 правило отделения, чтобы выяснить тот факт, что по меньшей мере в одном из квадратов [1,1], [2,2] или [3,1] есть яма: правило удаления двухсторонней импликации, после чего применить к полученному результату в сочетании с высказыванием R5 правило отделения, чтобы выяснить тот факт, что по меньшей мере в одном из квадратов [1,1], [2,2] или [3,1] есть яма: 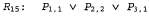
Именно здесь возникают условия, позволяющие впервые использовать правило резолюции (правило устранения противоречия): литерал в высказывании в высказывании , противоположный литералу , противоположный литералу в высказывании в высказывании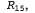 устраняется, что приводит к получению следующего высказывания: устраняется, что приводит к получению следующего высказывания: 
Соответствующий ход рассуждения можно выразить словами таким образом: если по меньшей мере в одном из квадратов [1,1], [2,2] или [3,1] имеется яма, но ее нет в квадрате [2,2], то яма должна быть, по крайней мере, в квадрате [1,1] или [3,1]. Аналогичным образом, устраняется литерал в высказывании в высказывании , противоположный литералу , противоположный литералу в высказываниичто в высказываниичто приводит к получению следующего высказывания: приводит к получению следующего высказывания: 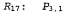
<< В начало < Предыдущая 1 2 3 4 5 6 Следующая > В конец >>
|