Еще более привлекательным свойством правила резолюции является то, что оно образует основу для семейства полных процедур логического вывода. Любой полный алгоритм поиска, в котором применяется только правило резолюции, позволяет вывести любое заключение, которое следует из любой базы знаний в пропозициональной логике. Тем не менее необходимо сделать одно предупреждение: правило резолюции является полным только в узком смысле этого понятия. Если известно, что высказывание А истинно, правило резолюции нельзя использовать для автоматического формирования следствия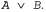Однако в этом случае правилом резолюции можно воспользоваться для поиска ответа на вопрос, является ли истинным высказывание Α ν Б. Это свойство правила резолюции называется полнотой опровержения (refutation completeness) и означает, что правило резолюции может всегда использоваться либо для подтверждения, либо для опровержения какого-то высказывания, но его нельзя применять для перебора всех истинных высказываний. В следующих двух подразделах описано, как может использоваться правило резолюции для осуществления логического вывода.

Конъюнктивная нормальная форма

Как было описано выше, правило резолюции применяется только к дизъюнкциям литералов, поэтому на первый взгляд оно распространяется только на базы знаний и запросы, состоящие из таких дизъюнкций. На каком же основании мы утверждаем, что это правило может служить основой процедуры полного логического вывода для всей пропозициональной логики? Ответ на этот вопрос состоит в том, что каждое высказывание пропозициональной логики логически эквивалентно конъюнкции дизъюнкций литералов. Любое высказывание, представленное как конъюнкция дизъюнкций литералов, называется высказыванием, находящимся в конъюнктивной нормальной форме, или CNF (Conjunctive Normal Form). Кроме того, ниже будет показано, что целесообразно определить также ограниченное семейство высказываний в конъюнктивной нормальной форме, называемое высказываниями в форме k-CNF. Высказывание в форме k-CNF имеет точно к литералов в расчете на каждое выражение: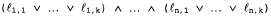

Как оказалось, любое высказывание может быть преобразовано в высказывание в форме 3-CNF, которое имеет эквивалентное множество моделей.