|
Страница 2 из 6 Соответствующий ход рассуждений можно выразить словами таким образом: если по меньшей мере в одном из квадратов [1,1] или [3,1] есть яма, но ее нет в квадрате [ 1,1 ], то она находится в квадрате [3,1]. Эти два последних этапа логического вывода представляют собой примеры применения правила логического вывода, называемого правилом единичной резолюции: 
где каждое из выражений представляет собой литерал, а выражения представляет собой литерал, а выражения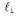 и т являются взаимно обратными литералами (т.е. такими литералами, что один из них является отрицанием другого). Таким образом, в правиле единичной резолюции берется выражение (дизъюнкция литералов) и еще один литерал, после чего формируется новое выражение. Обратите внимание на то, что этот единственный литерал может рассматриваться как дизъюнкция из одного литерала, называемая также единичным выражением. и т являются взаимно обратными литералами (т.е. такими литералами, что один из них является отрицанием другого). Таким образом, в правиле единичной резолюции берется выражение (дизъюнкция литералов) и еще один литерал, после чего формируется новое выражение. Обратите внимание на то, что этот единственный литерал может рассматриваться как дизъюнкция из одного литерала, называемая также единичным выражением. Правило единичной резолюции может быть также обобщено до правила полной резолюции: 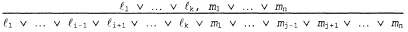
где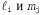 — взаимно обратные литералы. Если бы мы имели дело только с выражениями, имеющими длину два, то могли бы записать данное правило следующим образом: — взаимно обратные литералы. Если бы мы имели дело только с выражениями, имеющими длину два, то могли бы записать данное правило следующим образом: 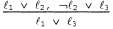
Это означает, что в правиле резолюции берутся два выражения и вырабатывается новое выражение, содержащее все литералы двух первоначальных выражений, за исключением двух взаимно обратных литералов. Например, может иметь место такой логический вывод: 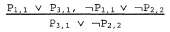
Процесс применения правила резолюции связан с необходимостью выполнения еще одного формального требования: результирующее высказывание должно содержать только по одной копии каждого литерала. Операция удаления дополнительных копий литералов называется факторизацией. Например, после удаления противоположных друг другу литералов в выражениях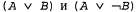 будет получено выражение будет получено выражение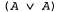 , которое следует сократить до А. , которое следует сократить до А. Непротиворечивость правила резолюции можно легко доказать, рассматривая литерал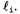 Если литерал Если литерал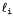 является истинным, то литерал является истинным, то литерал является ложным, и поэтому выражение является ложным, и поэтому выражение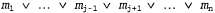 должно быть истинным, поскольку дано, что истинно выражение должно быть истинным, поскольку дано, что истинно выражение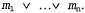 Если литерал Если литерал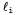 является ложным, то должно быть истинным выражение является ложным, то должно быть истинным выражение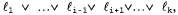 поскольку дано, что истинно выражение поскольку дано, что истинно выражение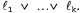 Итак, литерал Итак, литерал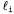 является либо истинным, либо ложным, поэтому справедливо одно или второе из этих заключений, а именно это утверждается в правиле резолюции. является либо истинным, либо ложным, поэтому справедливо одно или второе из этих заключений, а именно это утверждается в правиле резолюции.
|