Для повышения выразительной мощи моделей RPM применяется несколько способов. В частности, могут быть разрешены рекурсивные зависимости между переменными, позволяющие представить несколько типов зависимостей, которые ссылаются сами на себя. Например, предположим, что склонность к питанию всухомятку вызвана фактором McGene. В таком случае для любого х истинность выражения McGene(x) зависит от McGene (Father (x) ) и McGene (Mother (x) ), которые, в свою очередь, зависят от McGene (Fa ther (Fa ther (x) ) ), McGene (Mo ther (Fa ther (x) ) ), и т.д. Даже несмотря на то, что такие базы знаний соответствуют байесовским сетям с бесконечно большим количеством случайных переменных, иногда решения могут быть получены на основе уравнений с неподвижной точкой (fixed-point equation). Например, равновесное распределение вероятностей для генетического фактора McGene можно рассчитать на основе условной вероятности наследования этого фактора. Еще одно очень важное семейство рекурсивных баз знаний состоит из временных вероятностных моделей, которые описаны в главе 15. В этих моделях свойства рассматриваемого состояния во время t зависят от свойств этого состояния во время t-1 и т.д.

Модели RPM могут быть также расширены, чтобы в них можно было представить реляционную неопределенность, т.е. неопределенность, касающуюся значений сложных функций. Например, в базе знаний может отсутствовать информация о том, кто является консультантом Джонса, Advisor (Jones). В таком случае Advisor (Jones) становится случайной переменной с возможными значениями Prof Smi th и Prof Moore. Соответствующая сеть показана на рис. 14.11.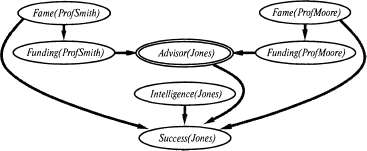

Рис. 14.11. Часть байесовской сеты, соответствующая одной из моделей RPM, в которой значение Advisor (Jones; неизвестно, но им может быть либо Prof Smith, либо Prof Moor е. Выбор студентом консультанта зависит от того, какой объем финансирования имеет каждый профессор. Обратите внимание на то, что теперь успех Джонса, Success (Jones), зависит от известности, Fame, обоих профессоров, хотя тот факт, какой из этих профессоров окажет влияние на успех Джонса, фактически зависит от значения переменной Advisor (Jones)

Модели RPM позволяют также представить такое свойство, как неопределенность идентичности (identity uncertainty); например, в базе знаний может отсутствовать информация о том, что Магу и ProfSmi th — одно и то же лицо. При наличии свойства неопределенности идентичности количество объектов и высказываний в разных возможных мирах может изменяться. В мире, где Магу и ProfSmi th — одно и то же лицо, количество объектов меньше, чем в том мире, где они считаются разными людьми. В результате этого процесс вероятностного вывода усложняется, но основные принципы, установленные в уравнении 14.12, все еще соблюдаются: вероятность любого высказывания вполне определена и может быть рассчитана. Свойство неопределенности идентичности является особенно важным для роботов и встроенных систем датчиков, которые должны следить за многими объектами. Мы вернемся к описанию этой проблемы в главе 15.