Характер модели восприятия для переменной BMetert заслуживает более глубокого анализа. Для упрощения предположим, что переменные могут принимать дискретные значения от 0 до 5, во многом аналогично измерительному прибору в типичном портативном компьютере, который применяется для контроля за аккумулятором. Если этот прибор всегда дает точные показания, то таблица условных вероятностейдолжна содержать вероятности 1. О в элементах, расположенных "вдоль диагонали", и вероятности 0 . О во всех других элементах. Но в действительности в результаты измерения всегда проникает шум, поэтому при использовании непрерывных измерений вместо этих результатов может использоваться гауссово распределение с небольшой дисперсией. Применительно к дискретным переменным, рассматриваемым в данном примере, гауссово распределение можно аппроксимировать с помощью распределения, в котором снижение вероятности ошибки соответствует реальной ситуации, поэтому вероятность крупной ошибки весьма мала. Мы будем использовать термин гауссова модель ошибки применительно и к непрерывной, и к дискретной версиям.

Те, кто имеет практический опыт работы в области робототехники, компьютеризированного управления процессами или в области применения других форм автоматического сбора информации, охотно подтвердят тот факт, что небольшие количества измерительного шума часто являются не самыми серьезными проблемами. Гораздо важнее то, что настоящие датчики отказывают, а когда датчик отказывает, он не всегда посылает сигнал с сообщением: "Между прочим, данные, которые я собираюсь вам отправить, можно считать бессмысленными". Вместо этого он просто передает бессмыслицу. Отказом простейшего типа является временный отказ, при котором датчик время от времени передает бессмысленные данные. Например, может оказаться, что датчик уровня зарядки аккумулятора имеет свойство передавать нулевое значение каждый раз, когда робот ударяется о препятствие, даже если аккумулятор полностью заряжен.

Рассмотрим, что произойдет при возникновении временного отказа, если используется гауссова модель ошибок, которая не приспособлена к таким отказам. Предположим, например, что робот спокойно ожидает и наблюдает за 20 последовательными показаниями датчика аккумулятора, равными 5. Затем датчик аккумулятора допускает временный сбой и передает следующее показание: К какому решению должна привести нас простая гауссова модель ошибки применительно к этому значению? Согласно правилу Байеса, ответ на этот вопрос зависит и от модели восприятия , и от предсказания 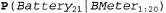. Если вероятность большой ошибки датчика является значительно менее правдоподобной, чем вероятность перехода в состояние , даже если последняя ситуация весьма неправдоподобна, то в распределении апостериорных вероятностей будет присвоена высокая вероятность той ситуации, что аккумулятор разряжен. Если же в момент времени t=22 будет получено еще одно показание, равное нулю, то такой вывод станет почти полностью безоговорочным. А после того, как этот временный отказ исчезнет и показания вернутся к 5, начиная с момента t=23 и продолжаясь в последующие моменты, то оценка уровня зарядки аккумулятора, как по волшебству, быстро вернется к 5. Такой ход событий проиллюстрирован на верхней кривой, приведенной на рис. 15.10, я, где показано ожидаемое изменение значения переменнойво времени при использовании дискретной гауссовой модели ошибки.