|
Страница 1 из 2 Как было указано выше, оператор Forward для фильтра Калмана отображает одно гауссово распределение на другое, новое гауссово распределение. Применение этого оператора сводится к вычислению новых значений среднего и матрицы кова-риации из предыдущих значений среднего и матрицы ковариации. Для вывода правила обновления в общем (многомерном) случае требуется большой объем выкладок в линейной алгебре, поэтому пока остановимся на очень простом одномерном случае, а позже будут даны результаты для общего случая. Но даже в одномерном случае вычисления являются довольно трудоемкими; тем не менее авторы считают, что с ними следует ознакомиться, поскольку применимость фильтра Калмана слишком тесно связана с математическими свойствами гауссовых распределений. Во временной модели, которая будет здесь рассматриваться, представлено случайное блуждание единственной непрерывной переменной состояния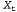 , зарегистрированное с помощью зашумленных результатов наблюдения , зарегистрированное с помощью зашумленных результатов наблюдения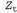 . Одним из соответствующих примеров может служить показатель "доверия потребителя", который может быть промоделирован как переменная, подвергающаяся каждый месяц случайному изменению с вероятностью, представленной с помощью гауссова распределения, и измеряемая с помощью опроса случайно выбранных потребителей, в котором также вносится гауссов шум формирования выборки. Предполагается, что распределение априорных вероятностей является гауссовым, с дисперсией . Одним из соответствующих примеров может служить показатель "доверия потребителя", который может быть промоделирован как переменная, подвергающаяся каждый месяц случайному изменению с вероятностью, представленной с помощью гауссова распределения, и измеряемая с помощью опроса случайно выбранных потребителей, в котором также вносится гауссов шум формирования выборки. Предполагается, что распределение априорных вероятностей является гауссовым, с дисперсией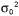 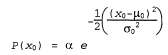
(Для упрощения в этом разделе мы будем использовать один и тот же символ α для обозначения всех констант нормализации.) В модели перехода просто добавляется гауссово возмущение постоянной дисперсии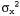 к текущему состоянию: к текущему состоянию: 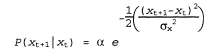
Это означает, что в модели восприятия должно быть принято предположение о наличии гауссова шума с дисперсией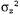 : : 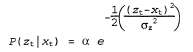
Теперь, после получения распределения априорных вероятностей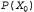 , мы можем , мы можем вычислить распределение, прогнозируемое на один этап, с помощью уравнения 15.15: 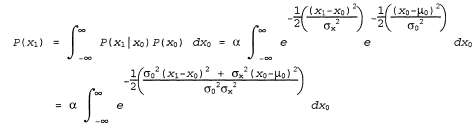
На первый взгляд этот интеграл кажется довольно сложным. Ключом к его упрощению может стать такое замечание, что экспонента представляет собой сумму двух выражений, которые квадратично зависят от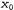 , и поэтому сама экспонента квадратично зависит от х0. Но известно, что любое квадратное уравнение , и поэтому сама экспонента квадратично зависит от х0. Но известно, что любое квадратное уравнение 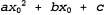 может быть перезаписано как сумма терма, возведенного в квадрат, может быть перезаписано как сумма терма, возведенного в квадрат,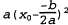 , и остаточного терма , и остаточного терма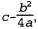 независимого от независимого от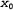 , с помощью преобразования, называе- , с помощью преобразования, называе- мого дополнением квадрата. Поэтому остаточный терм может быть вынесен за пределы интеграла, что приводит к получению следующего уравнения: 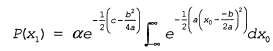
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|