До сих пор мы рассматривали только такие игры, которые состоят из одного хода. Простейшей разновидностью игры, состоящей из нескольких ходов, является повторяющаяся игра, в которой игроки снова и снова сталкиваются с одним и тем же выбором, но каждый раз пользуются знаниями истории всех предыдущих выборов всех игроков. Профиль стратегий для повторяющейся игры определяет выбор действия для каждого игрока на каждом временном интервале для всех возможных историй предыдущих выборов. Как и в случае задач MDP, вознаграждения определяются аддитивной функцией от времени.

Рассмотрим повторяющуюся версию поиска решения дилеммы заключенного. Будут ли Алиса и Боб действовать совместно и откажутся свидетельствовать друг против друга, зная о том, что им придется снова встретиться? Ответ зависит от деталей их соглашения. Например, предположим, Алиса и Боб знают, что им придется провести ровно 100 раундов игры в дилемму заключенного. В таком случае оба они знают, что 100-й раунд не будет повторяющейся игрой, т.е. что ее результат не сможет оказать влияния на будущие раунды, и поэтому оба они выберут в этом раунде доминантную стратегию testify. Но как только будет определен результат 100-го раунда, 99-й раунд перестанет оказывать влияние на последующие раунды, поэтому в нем также будет достигаться равновесие доминантной стратегии в случае выбора действий (testify, testify). По индукции оба игрока должны выбирать действие testify в каждом раунде, заработав общий срок по 500 лет тюремного заключения на каждого.

Изменяя правила взаимодействия, можно получить другие решения. Например, предположим, что после каждого раунда существует 99% шансов, что игроки снова встретятся. В таком случае ожидаемое число раундов все еще остается равным 100, но ни один из игроков не знает точно, какой раунд будет последним. При таких условиях возможно поведение, характеризующееся большей степенью сотрудничества. Например, одной из стратегий равновесия для каждого игрока является выбор действия refuse, если другой игрок никогда не выбирал действие testify Такую стратегию можно назвать вечным наказанием. Предположим, что оба игрока приняли данную стратегию и это известно им обоим. В таком случае, при условии, что ни один из игрок не выберет действие testify, в любой момент времени ожидаемое суммарное вознаграждение в будущем для каждого игрока составляет следующее: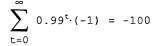

Игрок, который выберет testify, получит 0 очков вместо -1 в каждом следующем ходе, но его суммарное ожидаемое будущее вознаграждение становится равным: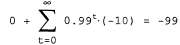