|
Страница 2 из 3 Каждая гипотеза предсказывает, что некоторое множество примеров (а именно множество тех примеров, которые соответствуют ее потенциальному определению) будет представлять собой примеры целевого предиката. Такое множество называется расширением предиката. Это означает, что две гипотезы с разными расширениями являются логически несовместимыми друг с другом, поскольку они не согласуются в своих предсказаниях по меньшей мере в одном примере. А если две гипотезы имеют одно и то же расширение, они логически эквивалентны. Пространство гипотез Η алгоритма обучения представляет собой множество всех гипотез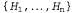 , для поддержки которых предназначен данный конкретный обучающий алгоритм. Например, алгоритм Decision-Tree-Learning способен поддерживать любую гипотезу в дереве решений, определенную в терминах заранее предусмотренных атрибутов, поэтому пространство гипотез этого алгоритма состоит из всех таких деревьев решений. Предполагается, что алгоритм обучения позволяет с полной уверенностью утверждать, что одна из гипотез является правильной; это означает, что данный алгоритм выражает определенную степень уверенности в истинности следующего высказывания: , для поддержки которых предназначен данный конкретный обучающий алгоритм. Например, алгоритм Decision-Tree-Learning способен поддерживать любую гипотезу в дереве решений, определенную в терминах заранее предусмотренных атрибутов, поэтому пространство гипотез этого алгоритма состоит из всех таких деревьев решений. Предполагается, что алгоритм обучения позволяет с полной уверенностью утверждать, что одна из гипотез является правильной; это означает, что данный алгоритм выражает определенную степень уверенности в истинности следующего высказывания: 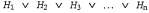 (19.2) (19.2)
По мере поступления новых примеров появляется возможность исключать гипотезы, не совместимые с этими примерами. Рассмотрим более внимательно затронутое здесь понятие совместимости. Очевидно, что если гипотеза совместима со всем обучающим множеством, то она должна быть совместимой с каждым примером. А что повлекла бы за собой его несовместимость с одним из примером? Такая ситуация может проявиться в одном из двух описанных ниже вариантов. совместима со всем обучающим множеством, то она должна быть совместимой с каждым примером. А что повлекла бы за собой его несовместимость с одним из примером? Такая ситуация может проявиться в одном из двух описанных ниже вариантов. • Некоторый пример может оказаться ложно отрицательным для данной гипотезы, если гипотеза утверждает, что он должен быть отрицательным, но фактически этот пример положителен. В частности, новый пример описанный выражением описанный выражением 
был бы ложно отрицателен для гипотезы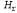 , приведенной выше. Из гипотезы , приведенной выше. Из гипотезы 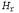 и описания этого можем вывести и выражение и описания этого можем вывести и выражение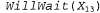 , которое как раз является утверждением данного примера, и выражение , которое как раз является утверждением данного примера, и выражение  , которое представляет собой предсказание самой гипотезы. Поэтому в данном случае гипотеза и пример логически несовместимы. , которое представляет собой предсказание самой гипотезы. Поэтому в данном случае гипотеза и пример логически несовместимы.
|