При использовании резолюции доказательство того, что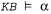(из базы знаний следует высказывание a) осуществляется путем доказательства невыполнимости выражения кв, т.е. путем получения пустого выражения. Алгоритмический подход, применяемый в логике первого порядка, идентичен подходу в пропозициональной логике, который показан в листинге 7.5, поэтому мы не будем здесь его повторять. Вместо этого приведем два примера доказательства. Первым из них является пример доказательства преступления, описанного в разделе 9.3. Соответствующие высказывания, преобразованные в форму CNF, выглядят следующим образом:

В число этих высказываний должна быть включена также отрицаемая цель . Процедура доказательства по методу резолюции показана на рис. 9.7. Обратите внимание на его структуру: единственный "хребет" начинается с целевого выражения, и операция резолюции применяется к выражениям из базы знаний до тех пор, пока не образуется пустое выражение. В этом состоит характерная особенность применения метода резолюции к базам знаний, представленным в виде хорновских выражений. В действительности выражения, расположенные вдоль главного хребта, точно соответствуют последовательным значениям целевых переменных в алгоритме обратного логического вывода, приведенном в листинге 9.3. Это связано с тем, что для резолюции всегда выбирается выражение, положительный литерал которого унифицируется с самым левым литералом "текущего" выражения в хребте; именно это происходит при обратном логическом выводе. Таким образом, обратный логический вывод в действительности представляет собой просто частный случай резолюции, в котором применяется конкретная стратегия управления для определения того, какая операция резолюции должна быть выполнена в следующую очередь.