В главе 13 было показано, что полное совместное распределение вероятностей позволяет отвечать на любые вопросы о рассматриваемой проблемной области, но может приобретать по мере увеличения количества переменных настолько большие размеры, что вычисления становятся невозможными. Более того, сам способ задания вероятностей для атомарных событий является довольно неестественным и может оказаться весьма затруднительным при отсутствии большого объема данных, на основании которых накапливаются статистические оценки.

Кроме того, в предыдущей главе было показано, что связи, определяющие независимость и условную независимость между переменными, позволяют намного сократить количество вероятностей, которые должны быть заданы в целях определения полного совместного распределения. В настоящем разделе показана структура данных, называемая1 байесовской сетью, которая позволяет представить связи между переменными и составить краткую спецификацию любого полного совместного распределения вероятностей.

Байесовская сеть — это ориентированный граф, в котором каждая вершина помечена количественной вероятностной информацией. Полная спецификация такой сети описана ниже.

1.    Вершинами сети является множество случайных переменных. Переменные могут быть дискретными или непрерывными.

2.    Вершины соединяются попарно ориентированными ребрами, или ребрами со стрелками; ребра образуют множество ребер. Если стрелка направлена от вершины X к вершине Y, то вершина X называется родительской вершиной вершины Y.

3.    Каждая вершина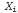характеризуется распределением условных вероятностей

, которое количественно оценивает влияние родительских вершин на эту вершину.

4.    Граф не имеет циклов, состоящих из ориентированных ребер (и поэтому является ориентированным ациклическим графом (Directed Acyclic Graph — DAG)).

Топология сети (множество вершин и ребер) показывает отношения, определяющие условную независимость, которые проявляются в данной проблемной области, в том смысле, который вскоре будет точно сформулирован. Интуитивный смысл стрелки в правильно составленной сети обычно состоит в том, что вершина X оказывает непосредственное влияние на вершину Y. Для специалиста в проблемной области задача определения того, какие непосредственные влияния существуют в этой проблемной области, обычно является довольно легкой; действительно, она намного легче по сравнению с фактическим определением самих вероятностей. После того как составлена топология байесовской сети, остается только указать распределение условных вероятностей для каждой переменной с учетом ее родительских переменных. В данной главе будет показано, что применение этой топологии и распределений условных вероятностей вполне позволяет (неявно) задать полное совместное распределение для всех переменных.

Еще раз вернемся к простому миру, описанному в главе 13, который состоит из переменных Toothache, Cavity, Catch и Weather. В этой главе было показано, что переменная Weather не зависит от других переменных; более того, было продемонстрировано, что переменные Toothache и Catch являются условно независимыми, если задана переменная Cavity. Эти отношения представлены в виде структуры байесовской сети, показанной на рис. 14.1. Формально условная независимость переменных Toothache и Catch, если задана переменная Cavity, обозначается отсутствием связи между Toothache и Catch. Интуитивно можно понять, что в сети представлен такой факт— Cavity является непосредственной причиной Toothache и Catch, тогда как между Toothache и Catch не существует прямой причинной связи.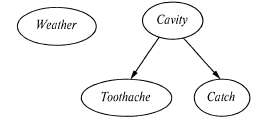

Рис. 14.1. Простая байесовская сеть, в которой переменная Weather независима от трех других переменных, а переменные Toothache и Catch являются условно независимыми, если задана переменная Cavity

Теперь рассмотрим следующий пример, который является немного более сложным. Житель пригорода установил в своем доме новую систему тревожной сигнализации для обнаружения взлома. Она довольно надежно обнаруживает взлом, но иногда также реагирует на небольшие землетрясения. (Этим примером мы обязаны Джуди Перлу, который живет в Лос-Анджелесе, поэтому проявляет острый интерес к землетрясениям.) У этого человека есть два соседа, Джон и Мэри, которые обещали звонить ему на работу, услышав тревожный сигнал. Джон всегда звонит, услышав тревожный сигнал, но иногда путает с ним телефонный звонок в доме соседа и в этих случаях также звонит. Мэри любит слушать довольно громкую музыку и поэтому иногда вообще пропускает тревожный сигнал. Получив факты о том, кто из этих соседей звонил или не звонил, необходимо оценить вероятность взлома. Байесовская сеть для этой проблемной области приведена на рис. 14.2.

На время отвлечемся от распределения условных вероятностей, показанных на этом рисунке, и сосредоточимся на топологии сети. В случае сети определения взлома топология показывает, что взлом и землетрясения непосредственно влияют на вероятность появления тревожного сигнала, а звонки Джона и Мэри зависят только от тревожного сигнала. Поэтому сеть подтверждает наши предположения, что соседи самостоятельно не обнаруживают какие-либо попытки взлома, не замечают незначительных землетрясений и не совещаются друг с другом перед звонками.

Обратите внимание на то, что в этой сети нет вершин, соответствующих тем ситуациям, в которых Мэри в настоящее время слушала бы громкую музыку или звонил бы телефон и сбивал с толку Джона. Эти факторы подытожены в показателях неопределенности, связанных с ребрами, направленными от вершины Alarm к вершинам JohnCalls и MaryCalls. Такая структура сети служит примером проявления в действии не только экономии усилий, но и недостатка знаний, поскольку потребовалось бы слишком много работы, чтобы узнать, по какой причине эти факторы могут оказаться более или менее вероятными в каждом конкретном случае; к тому же все равно отсутствует приемлемый способ получения релевантной информации. Вероятности, показанные на рисунке, фактически подытоживают потенциально бесконечное множество обстоятельств, которые либо могут вызвать нарушения при выработке тревожного сигнала (высокая влажность, отказ сети электропитания, разрядка аккумулятора, обрыв проводов, дохлая мышь, застрявшая внутри звонка, и т.д.), либо станут причиной того, что Джон или Мэри не смогут о нем сообщить (из-за того, что выйдут на обед, отправятся в отпуск, на время оглохнут, не расслышат сигнал в шуме пролетающего вертолета и т.д.). Но именно благодаря использованию приближенных оценок маленький агент получает возможность узнавать, что происходит в большом мире, по крайней мере, приблизительно. Степень приближения к истине может быть повышена по мере введения дополнительной релевантной информации.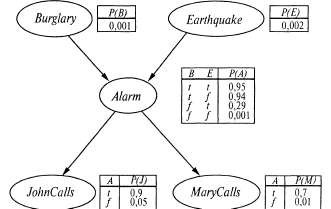

Рис. 14.2. Типичная байесовская сеть, на которой показаны и топология, и таблицы условных вероятностей (Conditional Probability Table — СРТ). В таблицах СРТ буквами В, Е, A, J и Μ обозначены следующие события: Burglary (Взлом), Earthquake (Землетрясение), Alarm (Тревожный сигнал), JohnCa11s (Звонки Джона) и МагуСа11s (Звонки Мэри)

Теперь обратимся к распределениям условных вероятностей, показанным на рис. 14.2. На этом рисунке каждое распределение представлено в виде таблицы условных вероятностей, или сокращенно СРТ (Conditional Probability Table). (Такая форма таблицы может использоваться для дискретных переменных; другие представления, включая те, которые подходят для непрерывных переменных, описаны в разделе 14.2.) Каждая строка в таблице СРТ содержит условную вероятность каждого значения вершины для обусловливающего случая (conditioning case), определяющего условную вероятность. Обусловливающий случай представляет собой одну из возможных комбинаций значений родительских вершин (в принципе его можно рассматривать как миниатюрное атомарное событие). Каждая строка должна в сумме составлять 1, поскольку элементы этой строки представляют собой исчерпывающее множество случаев для данной переменной. А если речь идет о булевых переменных, то после определения вероятности истинного значения, скажем р, вероятность ложного значения должна быть равна 1-р, поэтому в таблицах СРТ второе число часто не указывают, как и на рис. 14.2. Вообще говоря, любая таблица для булевой переменной с к булевыми родительскими переменными содержит 2к независимо определяемых вероятностей. Таблица для вершины без родительских вершин имеет только одну строку, представляющую априорные вероятности каждого возможного значения соответствующей переменной.