Вплоть до этого момента мы рассматривали все аспекты поиска, но игнорировали одно из наиболее важных усложнений в процессе поиска — вероятность появления непроизводительных затрат времени при развертывании состояний, которые уже встречались и были развернуты перед этим. При решении некоторых задач такая ситуация никогда не возникает; в них пространство состояний представляет собой дерево и поэтому имеется только один путь к каждому состоянию. В частности, эффективной является формулировка задачи с восемью ферзями (в которой каждый новый ферзь помещается на самый левый пустой вертикальный ряд), и ее эффективность в значительной степени обусловлена именно этим — каждое состояние может быть достигнуто только по одному пути. А если бы задача с восемью ферзями была сформулирована таким образом, что любого ферзя разрешалось бы ставить на любую вертикаль, то каждого состояния с п ферзями можно было бы достичь с помощью п! различных путей.

Таблица 3.2. Оценка стратегий поиска, где b — коэффициент ветвления; d — глубина самого поверхностного решения; т — максимальная глубина дерева поиска;— предел глубины. Предостережения, обозначенные строчными буквами, означают следующее:— полный, если коэффициент ветвления b конечен;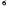— полный, если стоимость каждого этапапри некотором положительном значении е; — оптимальный, если стоимости всех этапов являются одинаковыми;— применимый, если в обоих направлениях осуществляется поиск в ширину

В некоторых задачах повторяющиеся состояния являются неизбежными. К ним относятся все задачи, в которых действия являются обратимыми, такие как задачи поиска маршрута и игры со скользящими фишками. Деревья поиска для этих проблем бесконечны, но если мы отсечем некоторые из повторяющихся состояний, то сможем уменьшить дерево поиска до конечного размера, формируя только ту часть дерева, которая охватывает весь граф пространства состояний. Рассматривая только часть дерева поиска вплоть до некоторой постоянной глубины, можно легко обнаружить ситуации, в которых удаление повторяющихся состояний позволяет достичь экспоненциального уменьшения стоимости поиска. В крайнем случае пространство состояний размером d+1 (рис. 3.11, а) становится деревом с 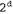листьями (рис. 3.11, б). Более реалистичным примером может служить прямоугольная решетка, как показано на рис. 3.11, в. 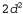В решетке каждое состояние имеет четырех преемников, поэтому дерево поиска, включающее повторяющиеся состояния, имеетлистьев, но существует приблизительно толькоразличных состояний с d этапами достижения любого конкретного состояния. Для d=20 это означает, что существует около триллиона узлов, но лишь примерно 800 различных состояний.