|
Страница 2 из 3 Таким образом, неспособность алгоритма обнаруживать повторяющиеся состояния может послужить причиной того, что разрешимая задача станет неразрешимой. Такое обнаружение обычно сводится к тому, что узел, подлежащий развертыванию, сравнивается с теми узлами, которые уже были развернуты; если обнаружено совпадение, то алгоритм распознал наличие двух путей в одно и то же состояние и может отбросить один из них. При поиске в глубину в памяти хранятся только те узлы, которые лежат на пути от корня до текущего узла. Сравнение этих узлов с текущим узлом позволяет алгоритму обнаружить зацикливающиеся пути, которые могут быть немедленно отброшены. Это позволяет обеспечить, чтобы конечные пространства состояний не превращались в бесконечные деревья поиска из-за циклов, но, к сожалению, не дает возможности предотвратить экспоненциальное разрастание нециклических путей в задачах, подобных приведенным на рис. 3.11. Единственный способ предотвращения этого состоит в том, что в памяти нужно хранить больше узлов. В этом заключается фундаментальный компромисс между пространством и временем. Алгоритмы, которые забывают свою историю, обречены на то, чтобы ее повторять. 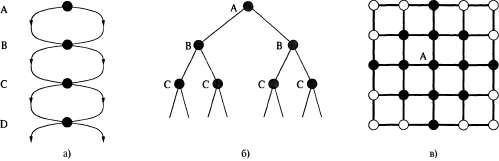 Рис. 3.11. Пространства состояний, которые формируют экспоненциально более крупные деревья поиска: пространство состояний, в котором имеются два возможных действия, ведущих от А к В, два — от В к С и т.д.; это пространство состояний содержит d+1 состояний, где d — максимальная глубина (а); дерево поиска, которое имеет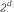 ветвей, соответствующих ветвей, соответствующих 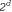 путям через это пространство (б); пространство состояний в виде прямоугольной решетки (в); состояния, находящиеся в пределах 2 этапов от начального состояния (А), обозначены серым цветом путям через это пространство (б); пространство состояний в виде прямоугольной решетки (в); состояния, находящиеся в пределах 2 этапов от начального состояния (А), обозначены серым цветом
|