Правило резолюции для выражений в логике первого порядка представляет собой поднятую версию правила резолюции для пропозициональной логики. Два выражения, которые, согласно принятому предположению, должны быть стандартизированными таким образом, чтобы в них не было общих переменных, могут быть подвергнуты операции резолюции, если они содержат взаимно дополнительные литералы. Пропозициональные литералы являются взаимно дополнительными, если один из них представляет собой отрицание другого, а литералы в логике первого порядка являются взаимно дополнительными, если один из них унифицируется с отрицанием другого. Поэтому имеет место следующее правило: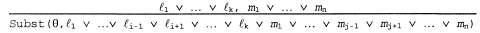

гдеНапример, можно применить операцию резолюции к следующим двум выражениям:

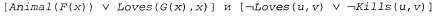
путем устранения взаимно дополнительных литералов Loves (G(x) , x) и с помощью унификатора для получения следующего выражения, называемого резольвентой: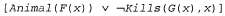

Только что приведенное правило называется правилом бинарной резолюции, поскольку в нем происходит удаление с помощью резолюции двух и только двух взаимно дополнительных литералов. Но правило бинарной резолюции, отдельно взятое, не позволяет получить полную процедуру логического вывода. С другой стороны, правило полной резолюции позволяет удалять в каждом выражении подмножества литералов, которые являются унифицируемыми. Альтернативный подход состоит в том, чтобы распространить операцию факторизации (удаления избыточных литералов) на логику первого порядка. В пропозициональной факторизации два литерала сводятся к одному, если они являются идентичными, а в факторизации первого порядка два литерала сводятся к одному, если они являются унифицируемыми.

Унификатор должен быть применен ко всему выражению. Сочетание бинарной резолюции и факторизации позволяет создать полную процедуру логического вывода