Например, три высказывания, приведенные выше, получены с помощью подстановок {x/John}, {x/ Richard) и {x/Father (John) }.

Соответствующее правило конкретизации высказывания с квантором существования (Existential Instantiation— EI) для квантора существования является немного более сложным. Для любых высказывания a, переменной ν и константного символа к, который не появляется где-либо в базе знаний, имеет место следующее: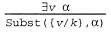

Например, из высказывания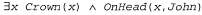

можно вывести высказывание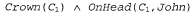

при условии, что константный символ С1 не появляется где-либо в базе знаний. По сути, в этом высказывании с квантором существования указано, что существует некоторый объект, удовлетворяющий определенному условию, а в процессе конкретизации просто присваивается имя этому объекту. Естественно, что это имя не должно уже принадлежать другому объекту. В математике есть прекрасный пример: предположим, мы открыли, что имеется некоторое число, которое немного больше чем 2,71828 и которое удовлетворяет уравнениюдля х. Этому числу можно присвоить новое имя, такое как е, но было бы ошибкой присваивать ему имя существующего объекта, допустим, п. В логике такое новое имя называется сколемовской константой. Конкретизация высказывания с квантором существования — это частный случай более общего процесса, называемого сколемизацией, который рассматривается в разделе 9.5.

Конкретизация высказывания с квантором существования не только сложнее, чем конкретизация высказывания с квантором всеобщности, но и играет в логическом выводе немного иную роль. Конкретизация высказывания с квантором всеобщности может применяться много раз для получения многих разных заключений, а конкретизация высказывания с квантором существования может применяться только один раз, а затем соответствующее высказывание с квантором существования может быть отброшено. Например, после того как в базу знаний будет добавлено высказывание Kill [Murderer, Victim), становится больше не нужным высказывание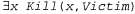. Строго говоря, новая база знаний логически не эквивалентна старой, но можно показать, что она эквивалентна с точки зрения логического вывода, в том смысле, что она выполнима тогда и только тогда, когда выполнима первоначальная база знаний.