|
Страница 2 из 2 Рассмотрим, почему так должно быть. Линия в сцене, проходящая через точку 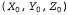 в направлении (U, V, W), может быть описана как множество точек в направлении (U, V, W), может быть описана как множество точек  , где λ изменяется в пределах от , где λ изменяется в пределах от . Проекция точки . Проекция точки от этой линии до плоскости изображения задается следующей формулой: от этой линии до плоскости изображения задается следующей формулой: 
По мере того как 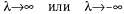 , эта формула принимает вид " , эта формула принимает вид "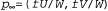 ' , если ' , если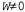 . Точку . Точку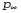 называют точкой схода, связанной с семейством прямых линий с ориентацией ( U, V, W). Все линии, имеющие одну и ту же ориентацию, имеют и одинаковую точку схода. называют точкой схода, связанной с семейством прямых линий с ориентацией ( U, V, W). Все линии, имеющие одну и ту же ориентацию, имеют и одинаковую точку схода. Если объект имеет относительно небольшую глубину по сравнению с его расстоянием от камеры, появляется возможность аппроксимировать перспективную проекцию с помощью масштабированной ортогональной проекции. Идея такой операции состоит в следующем: если глубина ζ точек объекта изменяется в некоторых пределах , то коэффициент перспективного масштабирования f/z можно приближенно представить с помощью константы , то коэффициент перспективного масштабирования f/z можно приближенно представить с помощью константы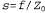 . Уравнения для проекции, которые связывают координаты сцены (Χ,Υ,Ζ) с координатами плоскости изображения, принимают вид x=sX и y=sY. Следует отметить, что масштабированная ортогональная проекция представляет собой аппроксимацию, действительную только для таких частей сцены, которые не характеризуются значительными изменениями внутренней глубины; эта проекция должна использоваться только для исследования свойств "в малом", а не "в большом". В качестве примера, позволяющего убедиться в необходимости соблюдать осторожность, отметим, что при использовании ортогональной проекции параллельные линии остаются параллельными, а не сливаются в точке схода! . Уравнения для проекции, которые связывают координаты сцены (Χ,Υ,Ζ) с координатами плоскости изображения, принимают вид x=sX и y=sY. Следует отметить, что масштабированная ортогональная проекция представляет собой аппроксимацию, действительную только для таких частей сцены, которые не характеризуются значительными изменениями внутренней глубины; эта проекция должна использоваться только для исследования свойств "в малом", а не "в большом". В качестве примера, позволяющего убедиться в необходимости соблюдать осторожность, отметим, что при использовании ортогональной проекции параллельные линии остаются параллельными, а не сливаются в точке схода!
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|