|
Страница 4 из 5 Допустим, что S' — конечное подмножество базовых высказываний. Теперь можно прибегнуть к базовой теореме резолюции, чтобы показать, что резо-люционное замыкание RC{Sf ) содержит пустое выражение. Это означает, что доведение до конца процесса пропозициональной резолюции применительно к S приводит к противоречию. Теперь, после определения того, что всегда существует доказательство по методу резолюции, в котором применяется некоторое конечное подмножество базы Эрбра-на множества 5, на следующем этапе необходимо показать, что существует доказательство по методу резолюции, в котором используются выражения из самого множества S, которые не обязательно являются базовыми выражениями. Начнем с рассмотрения одного приложения правила резолюции. Из базовой леммы Робинсона следует приведенный ниже факт. Допустим, что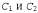 — два выражения без общих переменных, а — два выражения без общих переменных, а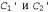 — базовые экземпляры — базовые экземпляры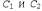 . Если . Если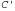 — резольвента — резольвента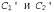 , то существует выражение с, такое, что, во-первых, С— резольвента , то существует выражение с, такое, что, во-первых, С— резольвента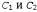 , и, во-вторых, С — базовый экземпляр с. , и, во-вторых, С — базовый экземпляр с. Это утверждение называется клеммой поднятия (lifting lemma), поскольку оно позволяет поднять любой этап доказательства от базовых выражений к общим выражениям в логике первого порядка. Для того чтобы доказать свою основную лемму поднятия, Робинсону пришлось изобрести унификацию и определить все свойства наиболее общих унификаторов. Мы здесь не будем повторять доказательство Робинсона, а просто проиллюстрируем применение этой леммы следующим образом: 
|