|
Страница 3 из 5 Итак, мы доказали (и сэкономили 29 с половиной страниц), что для любого множества истинных высказываний теории чисел и, в частности, для любого множества базовых аксиом существуют другие истинные высказывания, которые не могут быть доказаны из этих аксиом. Из этого, кроме всего прочего, следует, что мы никогда не сможем доказать все теоремы математики в пределах любой конкретной системы аксиом. Очевидно, что это открытие имело для математики очень важное значение. Значимость этого открытия для искусственного интеллекта была предметом широких обсуждений, начиная с размышлений самого Гёделя. Мы вступим в эти дебаты в главе 26. Для того чтобы выполнить первый этап доказательства, нам потребуются три новых понятия, описанных ниже. • Универсум Эрбрана. Если S— множество выражений, то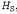 , универсум Эр-брана для множества S, представляет собой множество всех базовых термов, которые могут быть сформированы из следующего: , универсум Эр-брана для множества S, представляет собой множество всех базовых термов, которые могут быть сформированы из следующего: а) функциональные символы из множества S, если они имеются; б) константные символы из множества S, если они имеются; если они отсутствуют, то константный символ А. Например, если множество S содержит только выражение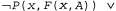 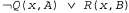 , то , то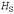 представляет собой следующее бесконечное множество базовых термов: представляет собой следующее бесконечное множество базовых термов: 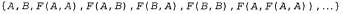
• Насыщение. Если S— множество выражений, а Р — множество базовых термов, то Ρ (S), насыщение S по отношению к р, представляет собой множество всех базовых выражений, полученное путем применения всех возможных совместимых подстановок базовых термов из Ρ вместо переменных в S. • База Эрбрана. Насыщение множества выражений S по отношению к его универсуму Эрбрана называется базой Эрбрана множества S и записывается как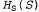 . Например, если S содержит только приведенное выше выражение, то . Например, если S содержит только приведенное выше выражение, то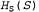 представляет собой следующее бесконечное множество выражений: представляет собой следующее бесконечное множество выражений: 
Эти определения позволяют сформулировать одну из форм теоремы Эрбрана[650]: Если множество выражений S является невыполнимым, то существует конечное подмножество HS (S), которое также является невыполнимым.
|