Полезность состояний определяется в терминах полезности последовательностей состояний. Грубо говоря, полезность любого состояния представляет собой ожидаемую полезность последовательностей состояний, которые могут привести к этому состоянию. Очевидно, что перечень таких последовательностей состояний зависит от осуществляемой стратегии, поэтому начнем с определения полезности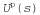по отношению к конкретной стратегии π. Если мы предположим, что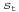— это состояние, в котором находится агент после осуществления стратегии π в течение t шагов (обратите внимание на то, что— случайная переменная), то получим следующее:

(17.3)

На основании этого определения можно утверждать, что истинная полезность любого состояния, которую обозначим как U{s), представляет собой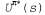, т.е. ожидаемую сумму обесцениваемых вознаграждений, при условии, что агент осуществляет оптимальную стратегию. Обратите внимание на то, что U(s) и R(s) — совершенно разные величины; R(s) — это "кратковременное" вознаграждение за пребывание в состоянии s; U(s) — "долговременное" суммарное вознаграждение, которое начинается с состояния s и продолжается дальше. На рис. 17.3 показаны рассматриваемые значения полезности для мира 4x3. Заслуживает внимание то, что значения полезности по мере приближения состояний к выходу +1 становятся выше, поскольку уменьшается количество шагов, требуемых для достижения этого выхода.

Рис. 17.3. Полезности состояний в мире 4x3, рассчитанные при y=1 u R(s)=-0.04 для нетерминальных состояний