|
Страница 2 из 2 Эта функция полезности u(s) позволяет агенту выбирать действия с использованием принципа максимальной ожидаемой полезности, приведенного в главе 16, т.е. выбирать действие, которое максимизирует ожидаемую полезность в следующем состоянии: 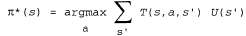 (17.4) (17.4)
Итак, если полезность некоторого состояния представляет собой ожидаемую сумму обесцениваемых вознаграждений, начиная с данного момента и дальше, то существует прямая связь между полезностью состояния и полезностью его соседних состояний: полезность некоторого состояния равна сумме непосредственного вознаграждения за пребывание в этом состоянии и ожидаемой обесцениваемой полезности следующего состояния, при условии, что агент выбирает оптимальное действие. Это означает, что полезность любого состояния можно определить с помощью следующего соотношения:  (17.5) (17.5)
Уравнение 17.5 называется уравнением Беллмана в честь Ричарда Беллмана [97]. Полезности состояний (определяемые с помощью уравнения 17.3 как ожидаемые полезности дальнейших последовательностей состояний) являются решениями множества уравнений Беллмана. В действительности, как будет показано в следующих двух разделах, они являются уникальными решениями. Рассмотрим одно из уравнений Беллмана для мира 4x3. Уравнение для состояния (1,1) приведено ниже. 
После подстановки в это уравнение чисел, приведенных на рис. 17.3, можно обнаружить, что наилучшим действием является Up.
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|