До сих пор приведенное выше описание поиска в ширину не предвещало никаких неприятностей. Но такая стратегия не всегда является оптимальной; чтобы понять, с чем это связано, необходимо определить, какое количество времени и какой объем памяти требуются для выполнения поиска. Для этого рассмотрим гипотетическое пространство состояний, в котором каждое состояние имеет Ь преемников. Корень этого дерева поиска вырабатывает b узлов на первом уровне, каждый из которых вырабатывает еще b узлов, что соответствует общему количеству узлов на втором уровне, равному . Каждый из них также вырабатывает Ъ узлов, что приводит к получению узлов на третьем уровне, и т.д. А теперь предположим, что решение находится на глубине d. В наихудшем случае на уровне d необходимо развернуть все узлы, кроме последнего (поскольку сам целевой узел не развертывается), что приводит к выработке 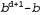узлов на уровне d+1. Это означает, что общее количество выработанных узлов равно:

Каждый выработанный узел должен оставаться в памяти, поскольку он либо относится к периферии, либо является предком периферийного узла. Итак, пространственная сложность становится такой же, как и временная (с учетом добавления одного узла, соответствующего корню).

Поэтому исследователи, выполняющие анализ сложности алгоритма, огорчаются (или восхищаются, если им нравится преодолевать трудности), столкнувшись с экспоненциальными оценками сложности, такими как . В табл. 3.1 показано, с чем это связано. В ней приведены требования ко времени и к объему памяти при поиске в ширину с коэффициентом ветвления b=10 для различных значений глубины решения d. При составлении этой таблицы предполагалось, что в секунду может быть сформировано 10 000 узлов, а для каждого узла требуется 1000 байтов памяти. Этим предположением приблизительно соответствуют многие задачи поиска при их решении на любом современном персональном компьютере (с учетом повышающего или понижающего коэффициента 100).