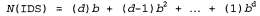
которая соответствует временной сложности порядка. Это количество можно сравнить с количеством узлов, формируемых при поиске в ширину: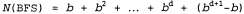

Рис. 3.9. Четыре итерации поиска с итеративным углублением в бинарном дереве

Следует отметить, что при поиске в ширину некоторые узлы формируются на глубине d+1, а при итеративном углублении этого не происходит. Результатом является то, что поиск с итеративным углублением фактически осуществляется быстрее, чем поиск в ширину, несмотря на повторное формирование состояний. Например, если b=10 и d=5, то соответствующие оценки количества узлов принимают следующие значения:

Вообще говоря, итеративное углубление — это предпочтительный метод неинформированного поиска при тех условиях, когда имеется большое пространство поиска, а глубина решения неизвестна.

Поиск с итеративным углублением аналогичен поиску в ширину в том отношении, что в нем при каждой итерации перед переходом на следующий уровень исследуется полный уровень новых узлов. На первый взгляд может показаться целесообразным разработка итеративного аналога поиска по критерию стоимости, который унаследовал бы от последнего алгоритма гарантии оптимальности, позволяя вместе с тем исключить его высокие требования к памяти. Идея состоит в том, чтобы вместо увеличивающихся пределов глубины использовались увеличивающиеся пределы стоимости пути. Результирующий алгоритм, получивший название поиска с итеративным удлинением, рассматривается в упр. 3.11. Но, к сожалению, было установлено, что поиск с итеративным удлинением характеризуется более существенными издержками, чем поиск по критерию стоимости.