•    Первый пример, X1, является положительным. Выражение Alternate(Х1) имеет истинное значение, поэтому допустим, что начальная гипотеза имеет такой вид: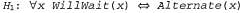

•    Второй пример, Х2, отрицателен. Гипотеза Η1 предсказывает, что он должен быть положительным, поэтому данный пример — ложно положителен. Это означает, что необходимо уточнить гипотезу H1. Это можно сделать, введя дополнительное условие, позволяющее исключить пример X2. Один из возможных вариантов состоит в следующем:

•    Третий пример, Х3 является положительным. Гипотеза H2 предсказывает, что он должен быть отрицательным, поэтому данный пример — ложно отрицательный. Это означает, что необходимо обобщить гипотезу Н2. Удалим условие А1 ternate и получим следующее:

•    Четвертый пример, Х4, также положителен. Гипотеза H3 предсказывает, что он должен быть отрицательным, поэтому данный пример — ложно отрицательный. Это означает, что необходимо обобщить гипотезу H3. Условие Patrons удалить нельзя, поскольку такая операция приведет к созданию всеохватывающей гипотезы, которая будет несовместимой с примером X2. Одна из возможностей состоит в добавлении дизъюнкта: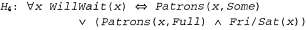

Итак, гипотеза уже начинает выглядеть как приемлемая. Очевидно, что есть и другие варианты, совместимые с первыми четырьмя примерами; ниже приведены два из них.

Алгоритм Current-Best-Learning описан здесь в недетерминированной форме, поскольку в любой момент может существовать возможность применить несколько вариантов уточнения или обобщения. Выбранный вариант не всегда обеспечивает получение простейшей гипотезы и может привести также к безвыходной ситуации, в которой ни одна простая модификация гипотезы не будет совместимой со всеми данными. В подобных случаях программа должна выполнить возврат к предыдущей точке выбора.

Алгоритм Current-Best-Learning и его варианты использовались во многих системах машинного обучения, начиная с программы "обучения распознаванию арок" Патрика Уинстона [1602]. Однако при большом количестве экземпляров примеров и большом пространстве гипотез возникают некоторые описанные ниже трудности.

1.    В алгоритме снова и снова проводится проверка всех предыдущих экземпляров при каждой модификации, а это требует больших затрат.

2.    Процесс поиска может быть связан с очень интенсивным перебором с возвратами. Как было показано в главе 18, размеры пространства гипотез могут определяться двойной экспоненциальной зависимостью.