|
Страница 3 из 4 Если же среда или стратегия является стохастической, задача становится более сложной. Предположим, что предпринимается попытка применить метод восхождения к вершине, для чего требуется сравнить ρ(θ) и ρ(θ+Δθ) при некотором небольшом значении ΔΘ. Проблема состоит в том, что суммарное вознаграждение при каждой попытке может существенно изменяться, поэтому оценки значения стратегии на основе небольшого количества попыток могут оказаться совершенно ненадежными, а еще более ненадежными становятся результаты, полученные при попытке сравнить две такие оценки. Одно из решений состоит в том, чтобы предпринять много попыток, измеряя дисперсию выборок и используя ее для определения того, достаточно ли много было сделано попыток, чтобы получить надежные данные о направлении улучшения для ρ (θ). К сожалению, такой подход является практически не применимым во многих реальных задачах, когда каждая попытка может оказаться дорогостоящей, требующей больших затрат времени, и, возможно, даже опасной. В случае стохастической стратегии существует возможность получить несмещенную оценку для градиента существует возможность получить несмещенную оценку для градиента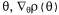 , соответствующего параметрам Θ, непосредственно по результатам попыток, выполненных при таких значениях параметра Θ. Для упрощения задачи выведем формулу такой оценки для простого случая непоследовательной среды, в которой вознаграждение предоставляется непосредственно после осуществления действия в начальном состоянии , соответствующего параметрам Θ, непосредственно по результатам попыток, выполненных при таких значениях параметра Θ. Для упрощения задачи выведем формулу такой оценки для простого случая непоследовательной среды, в которой вознаграждение предоставляется непосредственно после осуществления действия в начальном состоянии . В таком случае значение стратегии является просто ожидаемым значением вознаграждения, поэтому имеет место следующее: . В таком случае значение стратегии является просто ожидаемым значением вознаграждения, поэтому имеет место следующее: 
Теперь можно применить простой пример, позволяющий аппроксимировать результаты этого суммирования с помощью выборок, сформированных на основании распределения вероятностей, определенного стратегией . Предположим, . Предположим, что общее количество попыток равно N, а действием, предпринятым в j-й попытке, является . В таком случае получим следующее: . В таком случае получим следующее: 
Поэтому истинный градиент значения стратегии аппроксимируется суммой термов, включающей градиент вероятности выбора действия при каждой попытке. Для последовательного случая это соотношение можно обобщить до такого соотношения для каждого посещенного состояния s: 
где — действие, выполненное в состоянии s при j-й попытке; — действие, выполненное в состоянии s при j-й попытке;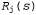 — суммарное вознаграждение, полученное, начиная от состояния s и дальше, при j-й попытке. Полученный в результате алгоритм называется Reinforce [1597]; обычно он является гораздо более эффективным по сравнению с восхождением к вершине, при котором используется большое количество попыток в расчете на каждое значение Θ. Тем не менее он все еще действует гораздо медленнее, чем абсолютно необходимо. — суммарное вознаграждение, полученное, начиная от состояния s и дальше, при j-й попытке. Полученный в результате алгоритм называется Reinforce [1597]; обычно он является гораздо более эффективным по сравнению с восхождением к вершине, при котором используется большое количество попыток в расчете на каждое значение Θ. Тем не менее он все еще действует гораздо медленнее, чем абсолютно необходимо.
|